Question

В правильной шестиугольной призме A...F1, все ребра которой равны 1, найдите угол между прямыми AB1 и CD1

Answer 1

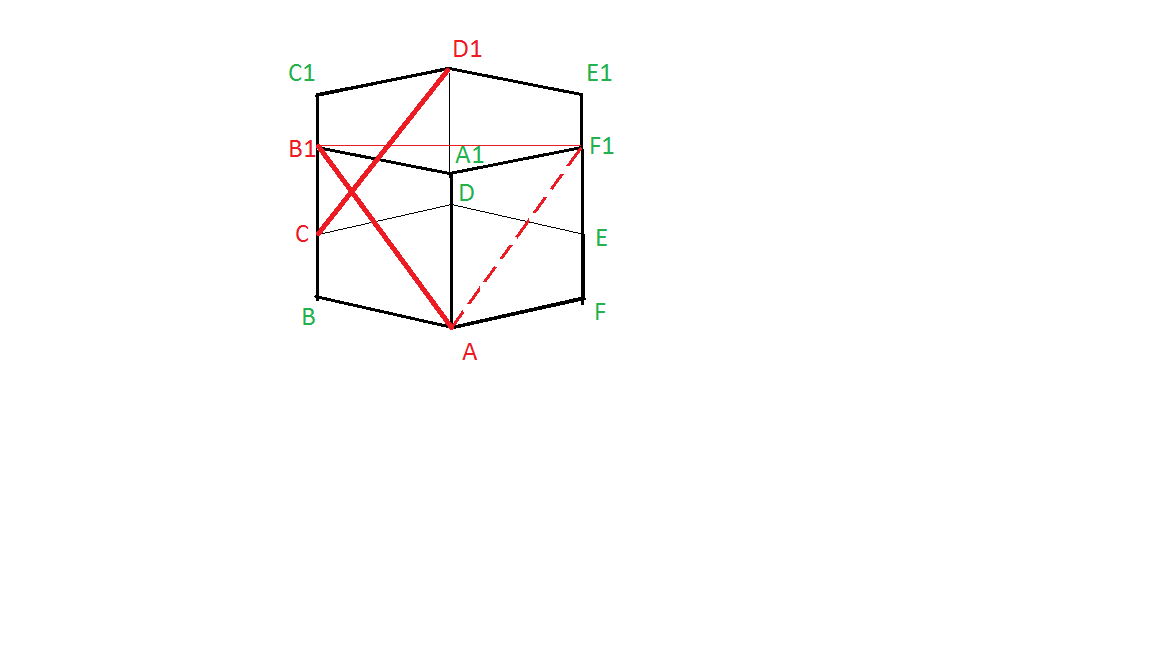
сделаем построение по условию
найдите угол между прямыми AB1 и CD1
РЕШЕНИЕ
Углы между прямой AB1  и любой прямой параллельной прямой CD1 будут равны.
Грани CDD1A1  и AFF1A1  параллельны и являются квадратами. CD1  и AF1 диагонали
этих граней, которые лежат в плоскости ACD1F1.
Сделаем параллельный перенос CD1  в AF1  и найдем угол  <B1AF1 равный искомому углу.
AB1 = AF1  - диагонали квадратов. По формуле Пифагора 
AB1 = AF1  = √ 1² + 1² = √2
В правильном шестиугольнике A1B1C1D1E1F1  все углы  120 град, тогда
в треугольнике B1A1F1  <B1A1F1  = 120 
По теореме косинусов  
B1F1² = DB1² + DF1² - 2*DB1*DF1*cos120
все ребра  равны  1
B1F1² = 1² + 1² - 2*1*1*cos120 = 3
По теореме косинусов  
B1F1² = AB1² + AF1² - 2*AB1*AF1*cos<B1AF1
cos<B1AF1 = (AB1² + AF1² - B1F1²) / (2*AB1*AF1)
cos<B1AF1 = (√2² + √2² - 3) / (2*1*1) = 1/2  = cos 60
<B1AF1 = 60 град  (или п/3)
ответ
60 град  (или п/3)