Question

ДАЮ 30 БАЛОВ СРОЧНО
................

Answer 1

4√3 см

Объяснение:

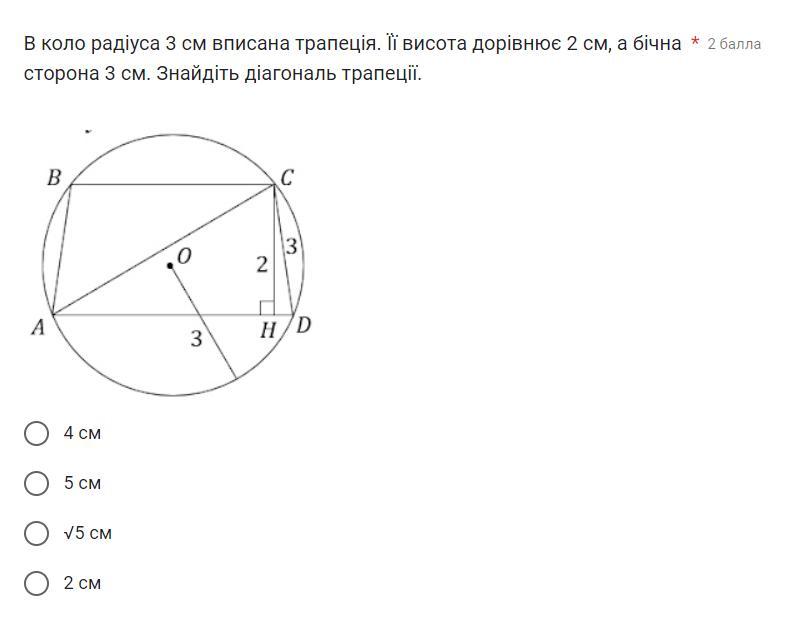
Трапеция вписана в окружность, значит она равнобедренная.

Диагонали равнобедренной трапеции равны.

Пусть ВС = х, тогда по условию:

АВ = ВС = CD = х, AD = 2x.

Проведем высоту СН. По свойству равнобедренной трапеции DH равен полуразности оснований:

�

�

=

�

�

−

�

�

2

−

2

�

−

�

2

=

�

2

DH=

2

AD−BC

−

2

2x−x

=

2

x

В прямоугольном треугольнике CHD катет равен половине гипотенузы, значит противолежащий угол 30°,

∠1 = 30°, ⇒ ∠2 = 60°

∠BAD = ∠2 = 60° (трапеция равнобедренная)

∠АВС = 180° - ∠BAD = 180° - 60° = 120°, так как сумма углов, прилежащих к боковой стороне трапеции, 180°.

ΔАВС равнобедренный,

∠

�

�

�

=

∠

�

�

�

=

18

0

∘

−

12

0

∘

2

=

6

0

∘

2

=

3

0

∘

∠BAC=∠BCA=

2

180

∘

−120

∘

=

2

60

∘

=30

∘

∠3 = ∠BAD - ∠BAC = 60° - 30° = 30°

В ΔADC ∠3 + ∠2 = 90°, значит он прямоугольный с гипотенузой AD.

ΔADC вписан в ту же окружность. Значит, AD - диаметр окружности.

AD = 4 · 2 = 8 см

Из прямоугольного треугольника ADC:

�

�

�

�

=

sin

⁡

6

0

∘

AD

AC

=sin60

∘

�

�

=

�

�

⋅

3

2

=

8

⋅

3

2

=

4

3

AC=AD⋅

2

3

=8⋅

2

3

=4

3