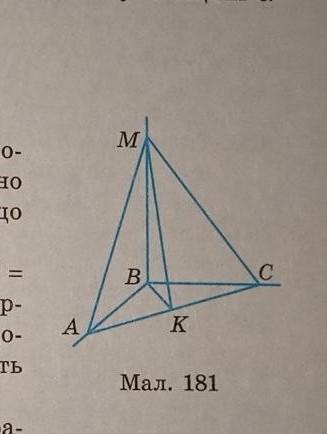
Трикутник АВС рівнобедрений, AB = BC = = 10 см, АС= 12 см. Пряма MB перпендикуляр- на до АВ і BC, K середина АС (мал. 181). До- ведіть, що ДMBK i MAK прямокутні. Знайдіть Їхні площі, якщо МВ = 15 см.
Ответы
Доказательство: Так как треугольник ABC равнобедренный, угол BAC = угол CAB = 90°. Таким образом, треугольник DMBK также будет иметь угол 90°, так как MB перпендикулярен AC.
Теперь найдем меру угла AMD:
Мы знаем, что К — середина АС, поэтому АК = 6 см.
Мы также знаем, что прямая MB перпендикулярна AB и BC, поэтому MK равна отрезку MB, который равен 15 см.
Теперь давайте посчитаем AM. Поскольку линия MB перпендикулярна линии AC, мы можем использовать теорему Пифагора для решения для AM
а^2 + б^2 = с^2
6^2 + 15^2 = АМ^2
90 + 225 = АМ ^ 2
315 = АМ ^ 2
Следовательно, АМ = √315 см
Стороны прямоугольного треугольника ABC равны сторонам AB = 10 см и AC = 12 см, следовательно, угол ABC = 90°.
Мы также знаем, что K является серединой AC, поэтому угол ACK = 45°.
Теперь вычислим меру угла АМК:
Мы знаем, что сумма углов треугольника равна 180º
угол АМК = 180º - 90º - 45º = 45º
Мы знаем меры угла AMK и угла DMBK.
Таким образом, треугольники DMBK и MAK оба прямоугольные.
Чтобы найти площади обоих треугольников, мы можем использовать формулу площади треугольника A = 1/2bh
Для треугольника DMBK b = 15 см и h = 6 см.
А = 1/2 × 15 см × 6 см = 45 см ^ 2
Для треугольника MAK b = MK = 15 см и h = AM.
A = 1/2 × 15 см × √315 см = 34,92 см^2
Следовательно, площадь треугольника DMBK равна 45 см^2, а площадь треугольника MAK равна 34,92 см^2.