Предмет: Алгебра,
автор: Viscount
Решите первый столбик неравенств
Приложения:
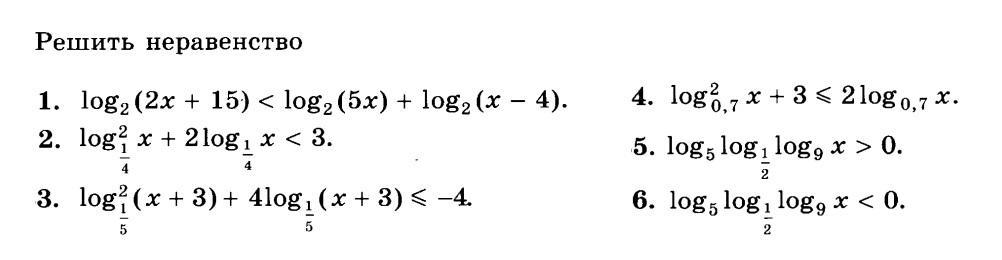
Ответы
Автор ответа:
1
Ответ:
1) x∈(5;+∞)
2) x∈(1/4;64)
3) x=22
Объяснение:
Для начала находим одз , зная , что аргумент логарифма должен быть строго больше нуля:
В правой части неравенства применим формулу суммы логарифмов с одинаковыми основаниями:
То есть:
Равны основания логарифмов , а это значит , равны и их аргументы:
Найдя пересечение с Одз , ответом будет
Одз : x>0
Пусть , тогда решим квадратное неравенство:
Вернёмся к обратной замене:
Ответ:
Одз:
Заменим , тогда будет иметь квадратное неравенство :
В левой части применим формулу сокращенного умножения (a+b)² = a²+2ab+b²:
Вернёмся к старой замене:
По одз подходит .
Ответ: x=22
Похожие вопросы
Предмет: Математика,
автор: hegxhsuevdhh
Предмет: Математика,
автор: a77430824
Предмет: Русский язык,
автор: thkhpvfpyf
Предмет: Математика,
автор: drybasburbon
Предмет: История,
автор: Аноним