Question

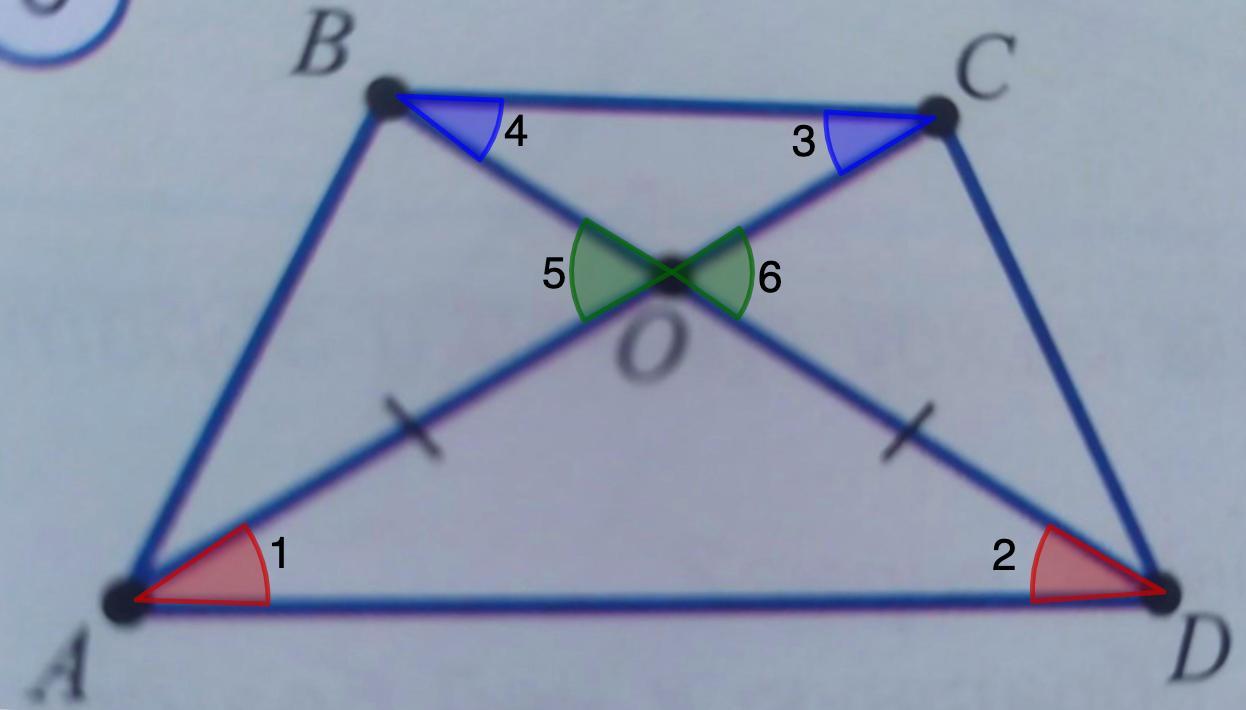
7. Известно, что BC||AD, AO=OD на рисунке 6. Докажите равенства: а) ВO=OC; b) AC=BD, c) АОВ=∆COD; d) АВD=∆ACD​

Answer 1

Ответ:

Доказано: а) ВO = OC; b) AC = BD, c) ΔАОВ = ∆COD; d) ΔАВD = ∆ACD​.

Объяснение:

7. Известно, что BC || AD, AO = OD на рисунке 6. Докажите равенства: а) ВO = OC; b) AC = BD, c) ΔАОВ = ∆COD; d) ΔАВD = ∆ACD​.

Дано: BC || AD, AO = OD;

Доказать: а) ВO = OC; b) AC = BD, c) ΔАОВ = ∆COD; d) ΔАВD = ∆ACD​.

Доказательство:

Для удобства обозначим углы цифрами (см.рис)

а) Рассмотрим ΔАОD.

АО = OD (условие)

• Если в треугольнике две стороны равны, то этот треугольник равнобедренный.

⇒ ΔАОD - равнобедренный.

• Углы при основании равнобедренного треугольника равны.

⇒ ∠1 = ∠2

Рассмотрим ΔВСО.

ВС || AD (условие)

⇒ ∠1 = ∠3 (накрест лежащие при ВС || AD и секущей АС);

∠2 = ∠4 (накрест лежащие при ВС || AD и секущей BD).

⇒ ∠3 = ∠4

• Если в треугольнике два угла равны, то этот треугольник равнобедренный.

⇒ ВО = ОС.

b) АО = OD (условие)

   ОС = ОВ  (п. а))

⇒ АО + ОС = ОD + ОВ

или АС = BD

c) Рассмотрим ΔАОВ и ∆COD.

АО = OD (условие)

ОС = ОВ  (п. а))

• Вертикальные углы равны.

⇒ ∠5 = ∠6 (вертикальные)

ΔАОВ = ∆COD (по двум сторонам и углу между ними, 1 признак)

⇒ АВ = CD (как соответственные элементы)

d) Рассмотрим ΔАВD и ∆ACD​.

AD = общая;

АС = BD (п.b))

AB = CD (п.с))

⇒ ΔАВD и ∆ACD​ (по трем сторонам, 3 признак)

#SPJ1