Предмет: Математика,
автор: anna518996g
Боковая сторона равнобедренного треугольника равен 12, высота, опущенная к основанию, равна 5. Найдите площадь
Ответы
Автор ответа:
1
Відповідь:
10√119
Покрокове пояснення:
У равнобедренного треугольника высота, опущенная к основанию, является также его медианой и высотой, соответственно она делит основание на два равных отрезка (медиана). По т. Пифагора можем найти один из этих одрезков: . Значит вся сторона равна
.
Площадь треугольника равна произведению стороны и высоты, опущенной к этой стороне: S = .
Приложения:
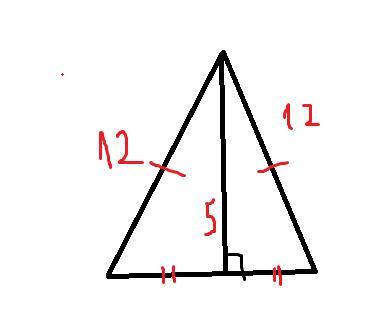
Похожие вопросы
Предмет: Українська література,
автор: 13didzlata
Предмет: Математика,
автор: aroslavaremenko24
Предмет: География,
автор: vaceslavmikolajchuk7
Предмет: Химия,
автор: jamilyakayumova
Предмет: История,
автор: 22548998896