Предмет: Алгебра,
автор: tutaevvadim4
СРОЧНО НУЖЕН ОТВЕТ!!
Приложения:
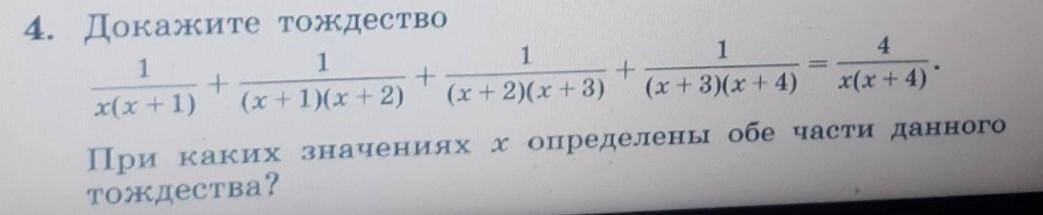
Ответы
Автор ответа:
0
Ответ:
(см. объяснение)
Объяснение:
Докажем, что верно:
Докажем базу индукции при :
, верно.
Докажем переход. Пусть равенство верно при .
Покажем его верность для :
Значит по принципу математической индукции доказываемое равенство верно.
Заметим, что исходное равенство есть доказанное нами при , а значит оно верно.
Обе части тождества определены при:
Задание выполнено!
Комментарий:
Заметим, что тождество не такое большое, поэтому возможно было бы выполнить преобразования вручную.
Однако мы доказали также, что, например:
А это вручную было бы считать уже проблематично.
Похожие вопросы
Предмет: Английский язык,
автор: ambambyoutub
Предмет: Биология,
автор: kurtanidzeviktoria94
Предмет: Алгебра,
автор: fariz999f
Предмет: Английский язык,
автор: shramkova0206
Предмет: Химия,
автор: chaiktv22