Предмет: Алгебра,
автор: student7513
Срочно 9 клас алгебра дяю 50 баловвв !!!!!!
Приложения:
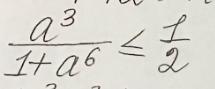
Ответы
Автор ответа:
0
Ответ:
на фото ......................
Приложения:

Автор ответа:
0
Ответ: a∈(-∞;+∞).
Объяснение:
ОДЗ:
Похожие вопросы
Предмет: Английский язык,
автор: semen24122011
Предмет: Другие предметы,
автор: MamKoTvK
Предмет: Английский язык,
автор: nottodaybts
Предмет: Алгебра,
автор: taisevashenko
Предмет: Математика,
автор: zavalin2007al