Предмет: Алгебра,
автор: ADHpepo
Алгебра 10 клас 1004 та 1006
Приложения:
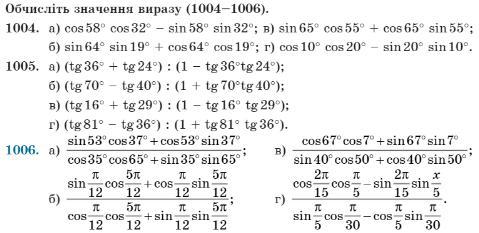
Ответы
Автор ответа:
2
Решение.
Применяем формулы синуса суммы и разности углов, а также
косинуса суммы и разности углов :
.
Похожие вопросы
Предмет: Английский язык,
автор: olegbespalko11
Предмет: Химия,
автор: liamm
Предмет: Алгебра,
автор: qabilcavadov25
Предмет: Немецкий язык,
автор: gohaogorodnikov
Предмет: Математика,
автор: ivannaydysh