Question

Помогите пожалуйста даю 100БАЛЛОВ
Алгебра 8 класс

Answer 1

Ответ:

Расстояние от пункта, из которого выехал первый самокатчик, до места встречи равно 68 км.

Объяснение:

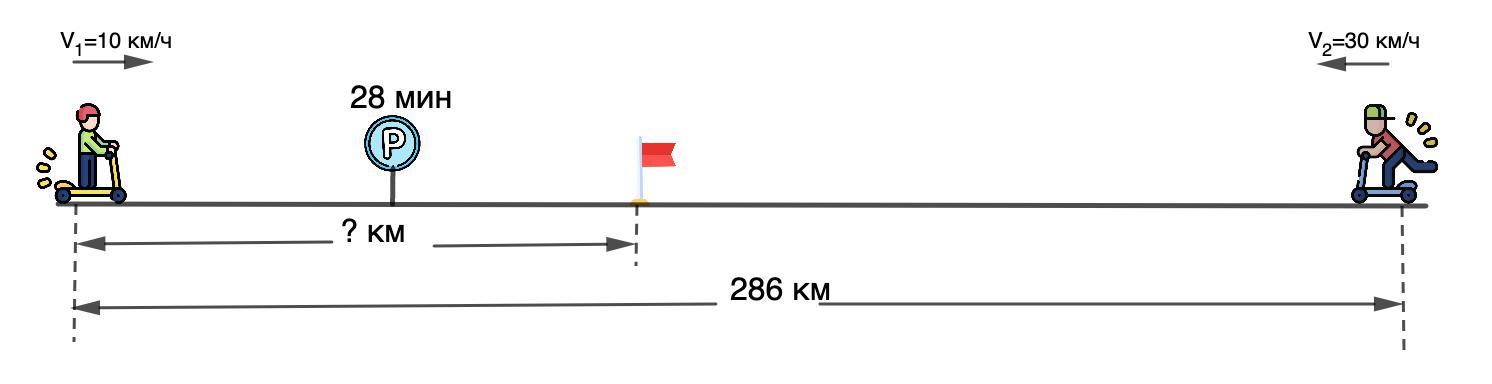
Из двух пунктов одновременно навстречу друг другу отправились два самокатчика. Проехав некоторую часть пути, первый самокатчик сделал остановку на 28 минут, а затем продолжил движение до встречи со вторым самокатчиком. Расстояние между пунктами составляет 286 км, скорость первого самокатчика равна 10 км/ч, скорость второго - 30 км/ч. Определите расстояние от пункта, из которого выехал первый самокатчик, до места встречи.

Так как самокатчики одновременно отправились из своих пунктов, то время до встречи у них одинаковое.

Пусть это время будет t часов.

Формула расстояния:

S = Vt,

где V - скорость, t - время.

Первый самокатчик сделал остановку 28 мин.

28 мин = 28/60 ч = 7/15 ч

Значит в движении он находился

$\displaystyle \bf \left(t-\frac{7}{15}\right)$ (ч)

Скорость его 10 км/ч.

И за это время он проехал расстояние до встречи:

$\displaystyle \bf S_1=10\cdot \left(t-\frac{7}{15}\right)$ (км)

Второй самокатчик ехал со скоростью 30 км t часов.

До встречи он проехал

$\displaystyle \bf S_2=30t$ (км)

Вместе они проехали 286 км.

Составим и решим уравнение:

$\displaystyle \bf S = S_1+S_2\\\\10\left(t-\frac{7}{15}\right) +30t=286\\\\10t-\frac{70}{15}+30t=286\\ \\ 40t=286+\frac{14}{3} \;\;\;\;\;|\cdot 3\\\\120t=872\;\;\;\;\;|:120\\\\t=\frac{109}{15}$

Теперь найдем S₁:

$\displaystyle \bf S_1=10\cdot \left(\frac{109}{15} -\frac{7}{15}\right)=10\cdot\frac{102}{15}=68$  (км)

Расстояние от пункта, из которого выехал первый самокатчик, до места встречи равно 68 км.