Question

допоможіть з геометрією ​

Answer 1

Ответ:

Объем пирамиды равен 81√3 см³.

Объяснение:

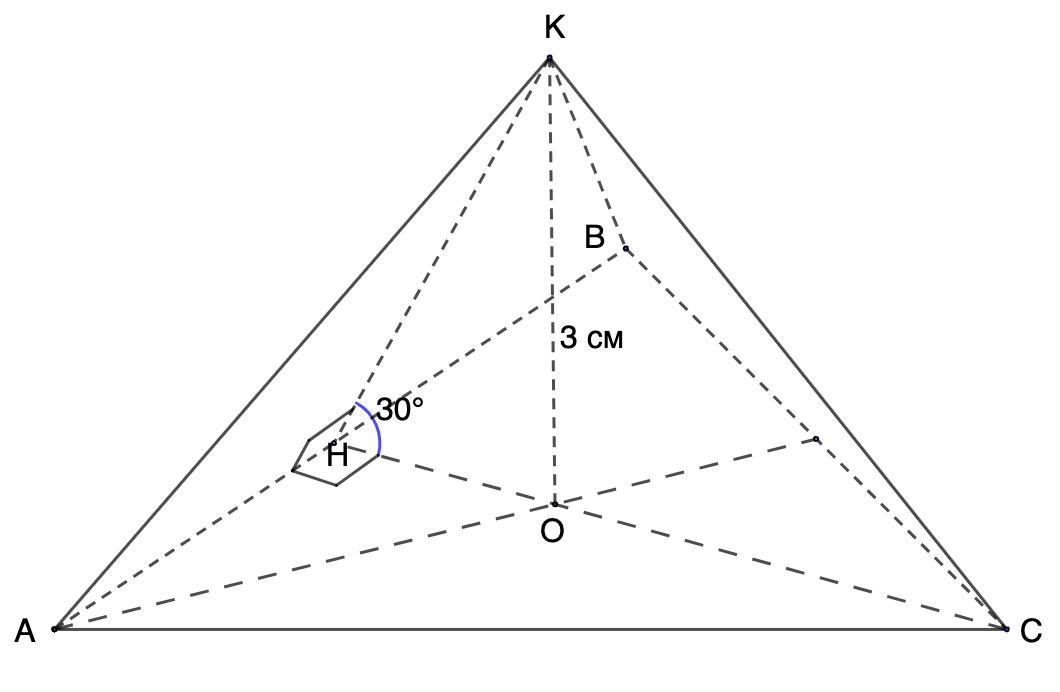
В правильной треугольной пирамиде боковые грани образуют с плоскостью основания угол 30°. Найдите объем пирамиды, если ее высота равна 3 см.

Дано: КАВС - правильная треугольная пирамида;

боковые грани образуют с плоскостью основания угол 30°;

КО = 3 см - высота.

Найти: V(КАВС)

Решение:

Объем пирамиды найдем по формуле:

$\boxed {\displaystyle \bf V=\frac{1}{3}\;S_{OCH} \cdot h}$

h = КО = 3 см

Надо найти площадь основания.

Так как пирамида правильная, то в основании лежит правильный треугольник и основание высоты лежит в точке пересечения медиан (высот, биссектрис)

Площадь равностороннего треугольника равна:

$\boxed {\displaystyle \bf S=\frac{a^2\sqrt{3} }{4}}$

1. Определимся с углом между гранью и основанием.

СН - высота ΔАВС.

Соединим точки Н и К.

ОН - проекция НК на плоскость АВС.

• Прямая, проведенная на плоскости через основание наклонной перпендикулярно ее проекции, перпендикулярна и самой наклонной.

⇒ КН ⊥ АВ

• Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей.

⇒ ∠КНО = 30°

2. Рассмотрим ΔНКО - прямоугольный.

• Котангенс угла - отношение прилежащего катета к противолежащему.

$\displaystyle \frac{HO}{OK}=ctg\;30^0\\ \\HO=3\cdot \sqrt{3}\;_{(CM) }$

3. Рассмотрим ΔАВС - равносторонний.

• Медианы треугольника точкой пересечения делятся в отношении 2:1, начиная от вершины.

⇒ НС = НО · 3 = 9√3 (см)

∠ВАС = 60°

• Синус угла - отношение противолежащего катета к гипотенузе.

$\displaystyle \frac{HC}{AC}=sin\;60^0 \\\\AC=\frac{9\sqrt{3} \cdot2}{\sqrt{3} } =18\;_{(CM)}$

4. Можем найти площадь ΔАВС:

$\displaystyle S=\frac{18^2\cdot\sqrt{3} }{4} =81\sqrt{3}\;_{(CM^2)}$

Объем КАВС равен:

$\displaystyle V=\frac{1}{3}\cdot 81\sqrt{3} \cdot3=81\sqrt{3}\;_{(CM^3)}$

Объем пирамиды равен 81√3 см³.

(скрины добавлены)