Question

Срочно!

У трикутнику МВР відомо, що МВ = 16см, ВР = 24см, МР = 32см. На
стороні МР взято точку К, так що РК = 9см. Знайти відрізок ВК.

Answer 1

Ответ: BK = 3√31 см

Объяснение:

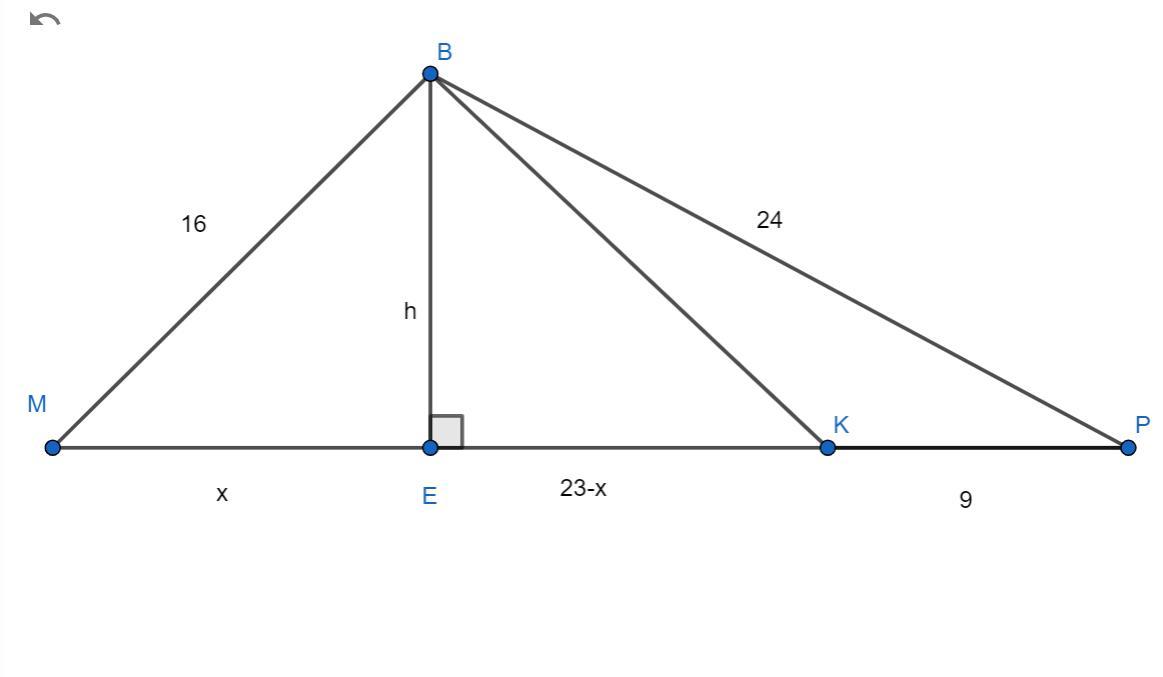
Строим ΔMBP , из вершины  B на основание MP проводим высоту  BE, которая будет делить MP , на отрезки  ME = x  , EP = 32 - x

Поскольку KP =  9 , то   EK = 32 - x - 9 = 23 - x

Рассмотрим прямоугольный ΔBPE ,  выразим   высоту BE = h    через x ,  с помощью  теоремы  Пифагора

BE² + EP² = BP²

h²  + (32 - x)² = 24²

h² = 24² - (32 - x)²

Также рассмотрим прямоугольный ΔMBE , снова применяем теорему Пифагора

BE² + ME² = MB²

h²  + x² = 16²

h²  =  16² - x²

Приравняем 24² - (32 - x)²   и  16² - x²

24² - (32 - x)²   =  16² - x²

(32 - x)²  -  x² = 24² -16²

(32 - x + x)(32 - x -x) = (24 + 16)(24-16)

32² -64x  = 40·8

64x = 32² - 320

64x = 16·64  - 64·5

x = 16 - 5

x = 11

Находим высоту

h² = 16² - x²

h² = 16² - 11²

h² = (16 + 11)(16 -11)

BE² = h² = 135

Теперь рассмотрим ΔBKE ,   с помощью теоремы Пифагора находим искомый отрезок  BK

BE² + EK² = BK²

h² + (23-x)² = BK²

BK² = 135 + (23-11)²

BK²  = 135 + 144

BK² = 279

BK = 3√31(см)

#SPJ1