Question

Помогите пожалуйста!

Задача 4.

Для заданной функции

у = (x^2+x)*e^x

1) найти точки экстремума и определить интервалы монотонности функции:

2) найти точки перегиба и интервалы выпуклости функции;

3) найти асимптоты и построить график функции.

Answer 1

Ответ:

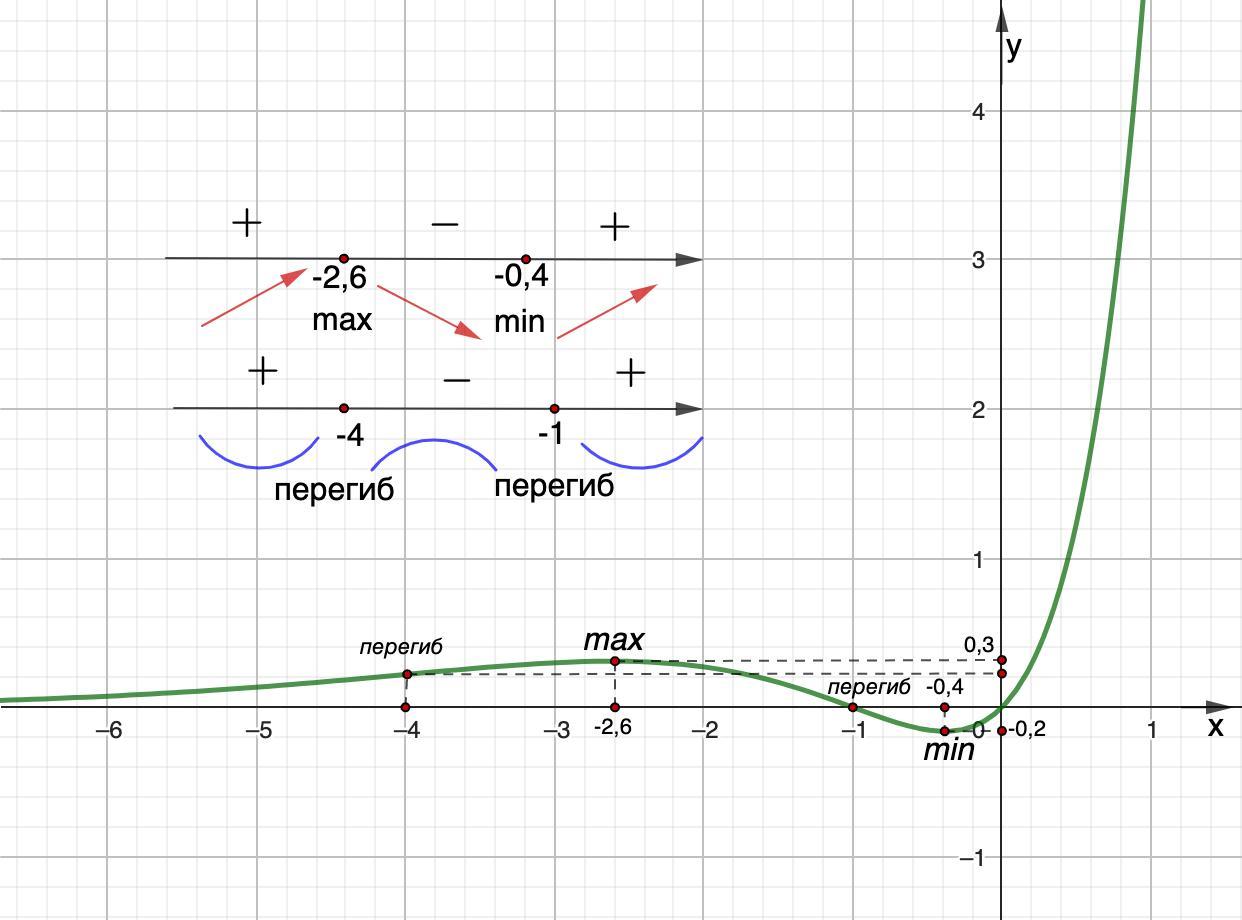
1) Функция возрастает на промежутках: (-∞; -2,6]; [-0,4; +∞)

Функция убывает на промежутке: [-2,6; -0,4]

$\displaystyle x_{max}=-2,6;\;\;\;\;\;x_{min}=-0,4$

2) Функция вогнута на промежутках: (-∞; -4]; [-1; +∞)

Функция выпукла на промежутке: [-4; -1]

х перегиба = {-4; -1}

3) y = 0 - горизонтальная асимптота.

Пошаговое объяснение:

Для заданной функции

у = (x²+x) · eˣ

1) найти точки экстремума и определить интервалы монотонности функции:

2) найти точки перегиба и интервалы выпуклости функции;

3) найти асимптоты и построить график функции.

Дана функция: $\displaystyle \bf y=(x^2+x)\cdot e^x$

1) Для того чтобы найти точки экстремума и определить интервалы монотонности функции, найдем производную, приравняем к нулю и найдем корни.

$\displaystyle y'=(2x+1)\cdot e^x+(x^2+x)\cdot e^x=e^x(x^2+3x+1)$

$\displaystyle y'=0;\;\;\;\;\;e^x(x^2+3x+1)=0\\\\e^x > 0\;\;\;\Rightarrow \;\;\;x^2+3x+1=0\\\\D=9-4=5\;\;\;\;\;\sqrt{D}=\sqrt{5} \\\\x_1=\frac{-3+\sqrt{5} }{2}\approx -0,4;\;\;\;\;\;x_2=\frac{-3-\sqrt{5} }{2}\approx -2,6$

Отметим корни на числовой оси и определим знаки производной на промежутках.

• Если "+" - функция возрастает, если "-" - функция убывает.

См. вложение.

Функция возрастает на промежутках: (-∞; -2,6]; [-0,4; +∞)

Функция убывает на промежутке: [-2,6; -0,4]

• Если производная меняет знак с плюса на минус, то в данной точке наблюдается максимум, если с минуса на плюс, то в данной точке  - минимум.

⇒ $\displaystyle x_{max}=-2,6;\;\;\;\;\;x_{min}=-0,4$

y(-2.6) ≈ 0,3;     y(-0,4)≈-0,2

2) Для того чтобы найти точки перегиба и интервалы выпуклости функции, найдем производную второго порядка, приравняем к нулю и найдем корни.  

$\displaystyle y''=e^x(x^2+3x+1)+e^x(2x+3)=e^x(x^2+5x+4)\\\\e^x > 0;\;\;\;\Rightarrow \;\;\;x^2+5x+4=0$

По теореме Виета:

$\displaystyle x_1=-4;\;\;\;\;\;x_2=-1$

Отметим эти корни на числовой оси и определим знаки второй производной на промежутках.

См. вложение.

• Если производная второго порядка положительна, функция вогнута, если отрицательна - выпукла.

Функция вогнута на промежутках: (-∞; -4]; [-1; +∞)

Функция выпукла на промежутке: [-4; -1]

• Точки, в которых вторая производная меняет знак, называют точками перегиба.

х перегиба = {-4; -1}

y(-4) ≈ 0,2;     y(-1) = 0

3) Найдем асимптоты.

D(y) = x ∈ R   ⇒   вертикальных асимптот нет.

Наклонные у = kx + b

$\displaystyle k= \lim_{x \to \infty} \frac{(x^2+x)e^x}{x}= \infty}$

⇒ при x → +∞ наклонных асимптот нет.

Найдем наклонную асимптоту при х → -∞:

$\displaystyle k= \lim_{x \to- \infty} ((x^2+x)e^x)= 0\\\\b= \lim_{x \to- \infty} ((x^2+x)e^x-0)= 0$

⇒ y = 0 - горизонтальная асимптота.

Строим график.

#SPJ1