Предмет: Геометрия,
автор: Evgenia4836
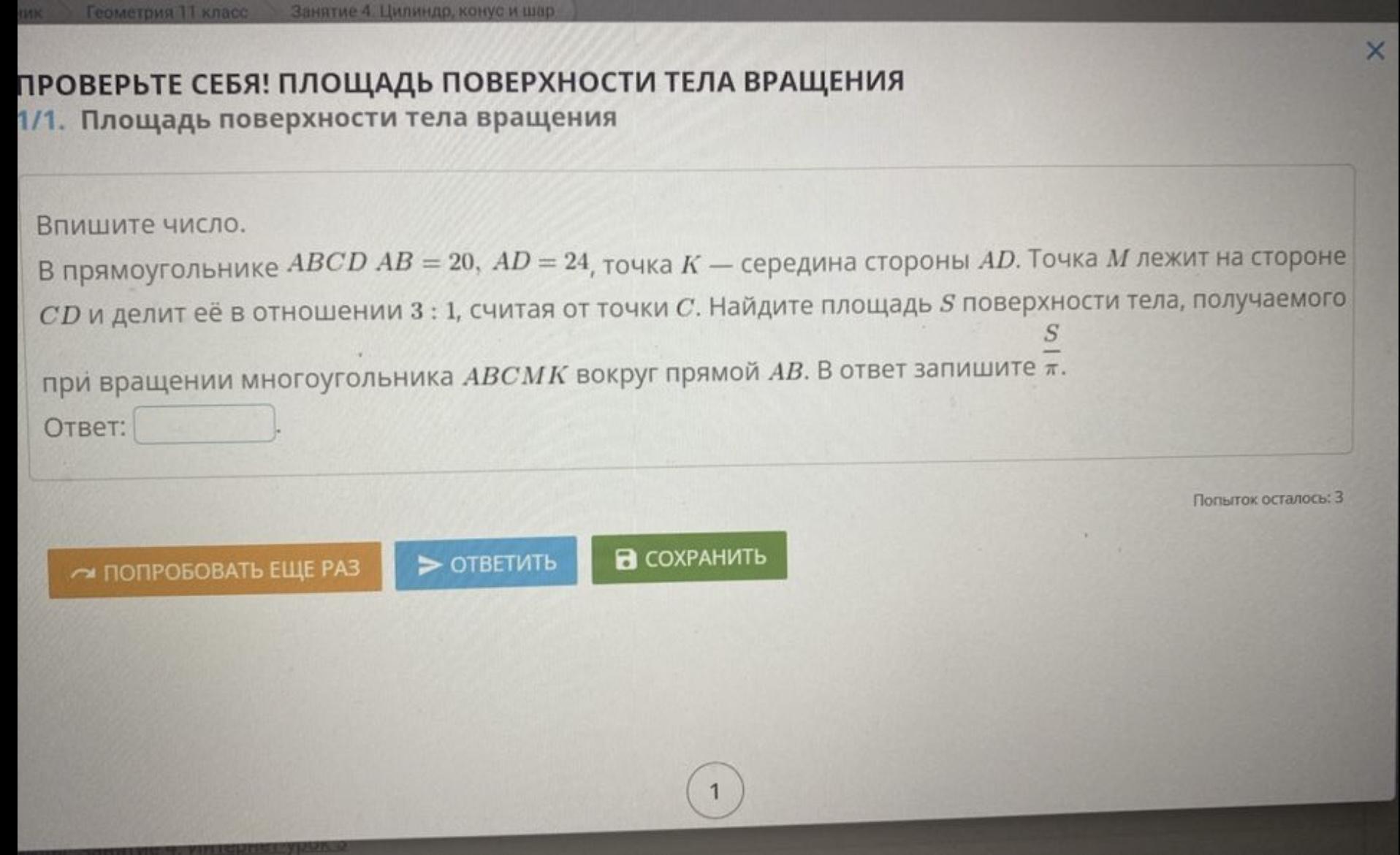
Площадь поверхности тела вращения
Приложения:
Ответы
Автор ответа:
1
Прямоугольник ABCD является основанием тела, получаемого при вращении многоугольника ABCMK вокруг прямой AB. Поскольку AB - это диаметр основания, то радиус этого основания равен AB/2 = 20/2 = 10.
Теперь нам нужно найти площадь поверхности тела, получаемого при вращении многоугольника ABCMK вокруг прямой AB. Эта площадь равна площади основания умноженной на длину обхвата.
Длина обхвата тела равна длине многоугольника ABCMK. Длина стороны AB равна 20, а длина стороны AD равна 24. Таким образом, длина многоугольника ABCMK равна 24 + 20 = 44.
Теперь мы можем найти площадь поверхности тела, получаемого при вращении многоугольника ABCMK вокруг прямой AB: S = Pi * r^2 * L = Pi * 10^2 * 44 = 4400 * Pi.
Ответ: S/Pi = 4400.
Похожие вопросы
Предмет: Алгебра,
автор: alexandrbarnett79
Предмет: Английский язык,
автор: sandra438671
Предмет: Українська мова,
автор: orosanastasia40
Предмет: Английский язык,
автор: jojakoma115566
Предмет: Химия,
автор: juliaz14122006