Question

Кто нибудь пжжж срочно помогите!!!! 2 и 3 задания!!!!

Answer 1

Ответ:

2) Расстояние между окружностью x²+y²+y=0 и началом координат равно 0

3) $\tt S_{sektor} = 37,5 \cdot \pi$, $\tt S_{segment} = 37,5 \cdot \pi - 25 \cdot \sqrt{2}$

Пошаговое объяснение:

Нужно знать: Центральный угол всегда равен градусной мере дуги, на которую он опирается.

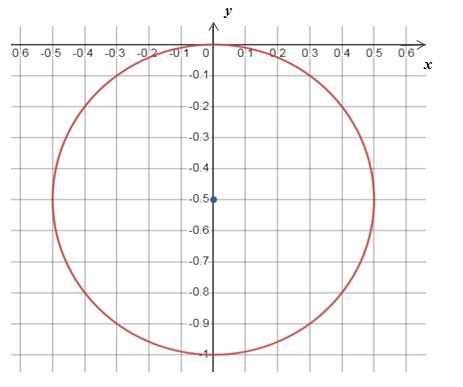
2) Найти расстояние между окружностью x²+y²+y=0 и началом координат.

Приведём уравнение окружности в канонический вид:

$\tt \displaystyle x^2+y^2+y=0\\\\x^2+y^2+2 \cdot \frac{1}{2} \cdot y+(\frac{1}{2} )^2-(\frac{1}{2} )^2=0 \\\\x^2+(y+\frac{1}{2} )^2=(\frac{1}{2} )^2.$

Из последнего уравнения следует, что центр окружности находится в точке (0; -0,5) и радиус окружности R = 0,5 (см. рисунок). Но окружность проходит через начало координат и поэтому расстояние между окружностью x²+y²+y=0 и началом координат равно 0.

Если нужно определить расстояние между центром окружностью x²+y²+y=0 и началом координат, то оно равно 0,5.

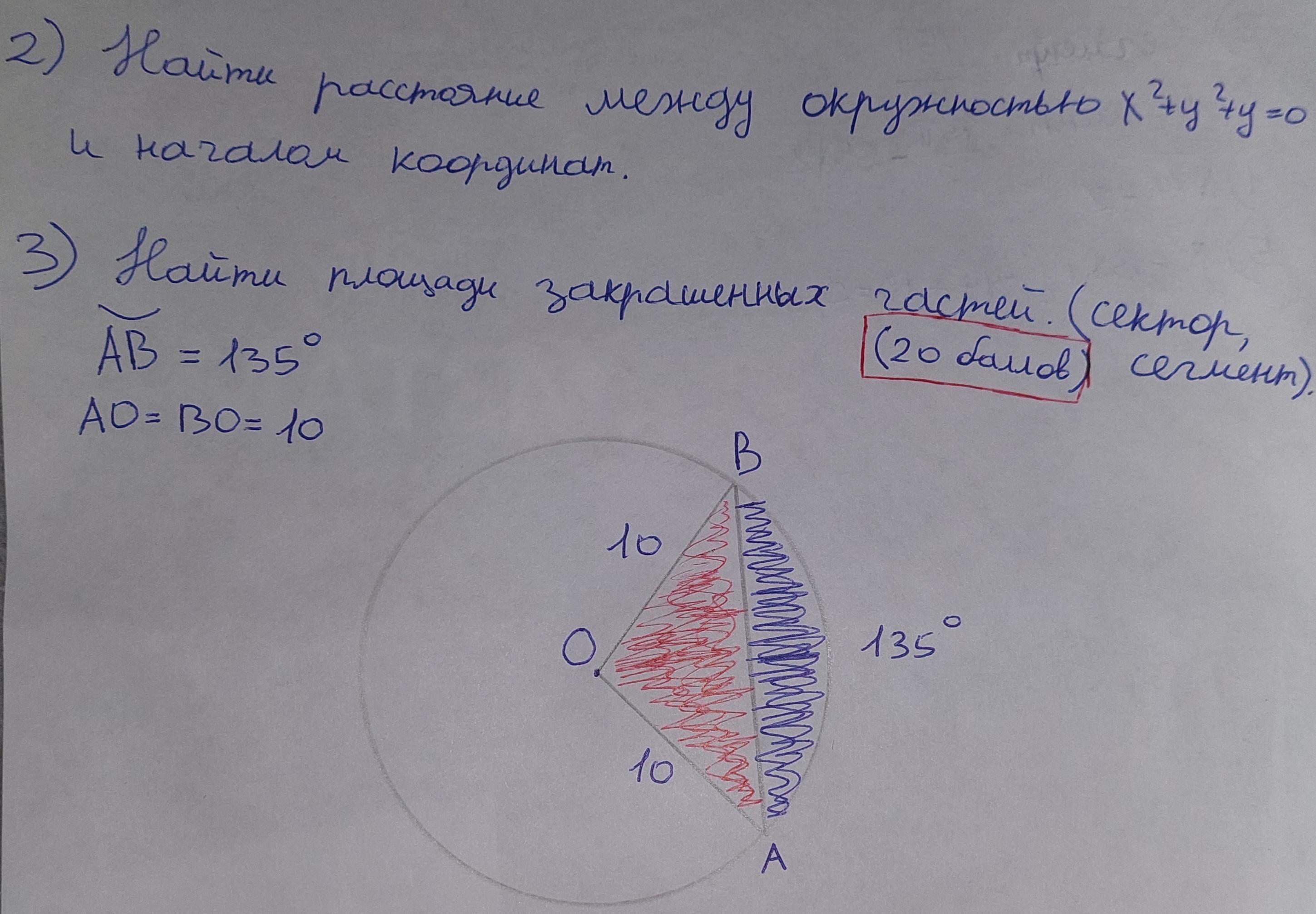
3) Площадь кругового сектора угла α круга радиуса R определяется по формуле

$\tt S_{sektor} = \dfrac{\pi \cdot R^2 \cdot \alpha }{360^0} .$

Так как α = 135° и R = 10, то

$\tt S_{sektor} = \dfrac{\pi \cdot 10^2 \cdot 135^0 }{360^0} =\dfrac{\pi \cdot 100 \cdot 3 }{8} = 37,5 \cdot \pi .$

Площадь кругового сегмента угла α круга радиуса R определяется по формуле

$\tt S_{segment} = \dfrac{\pi \cdot R^2 \cdot \alpha }{360^0} -\dfrac{1}{2} \cdot R^2 \cdot sin \alpha .$

Поэтому площадь кругового сегмента в нашем случае равна

$\tt S_{segment} = 37,5 \cdot \pi -\dfrac{1}{2} \cdot 10^2 \cdot sin 135^0=37,5 \cdot \pi -\dfrac{1}{2} \cdot 100 \cdot \dfrac{\sqrt{2} }{2} =37,5 \cdot \pi - 25 \cdot \sqrt{2} .$

#SPJ1