Пожалуйста решите детально желательно на бумаге и без Photomath!
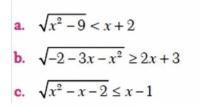
Ответы
Ответ:
a) Ответ: [3; +∞)
b) Ответ:
c) Ответ: [2; 3]
Пошаговое объяснение:
Решить неравенства:
Сначала ОДЗ.
Подкоренное выражение неотрицательно.
х² - 9 ≥ 0
(х - 3)(х + 3) ≥ 0
x ∈ (-∞;-3] ∪ [3; +∞)
Так как левая часть неотрицательная и меньше правой части, то правая часть должна быть только положительной.
х + 2 > 0 ⇒ x > -2
x ∈ (-2; + ∞)
⇒ D(y) = [3; +∞)
Теперь можем возвести в квадрат обе части:
- Если обе части неравенства умножить или разделить на отрицательное число, знак неравенства перевернется.
Объединим с ОДЗ.
Ответ: [3; +∞)
ОДЗ: -2 - 3х - х² ≥ 0
-(х² + 3х + 2) ≥ 0
х₁ = -1; х₂ = -2
x ∈ [-2; -1]
Левая часть неотрицательна и больше правой части. Здесь может быть два варианта:
1)
2)
Решим второе неравенство:
Решим методом интервалов:
Получим:
Решением системы будет савокупность неравенств:
Ответ:
ОДЗ:
Решим первое неравенство методом интервалов.
х² - х - 2 = 0
х₁ = 2; х₂ = -1
x ∈ (-∞; -1] ∪ [2; +∞)
Решение второго неравенства:
х ≥ 1 или х ∈ [1; +∞)
⇒ D(y) = [2; +∞)
Возведем в квадрат обе части неравенства:
Объединим с ОДЗ.
Ответ: [2; 3]