Question

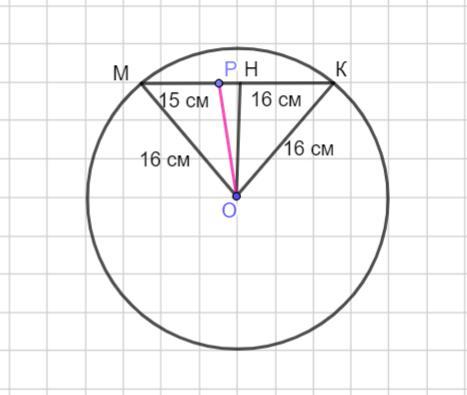
Хорда МК ділиться точкою Р на два відрізки завдовжки 15 см і 16 см. Знайдіть відстань від точки р до центра кола, його радіус дорівнює 16 см.

Answer 1

Ответ:

Расстояние от точки Р  до центра окружности равно 4 см.

Объяснение:

Хорда МК делится точкой Р на два отрезка длиной 15 см и 16 см . Найдите расстояние от точки Р до центра окружности, радиус которой равен 16 см.

Пусть дана окружность с центром в точке О радиуса 16 см и хорда МК .

Тогда ОК =ОМ  = 16 см. Точка Р лежит на хорде МК, так что МР = 15 см, а РК =16 см.

Рассмотрим Δ МОК - равнобедренный , так как МО =КО = 16 см.

МК = МР +РК;

МК =15 +16 =31 см.

В равнобедренном треугольнике проведем высоту ОН , проведенную к основанию. Высота ОН является медианой. Тогда МН =КН = 31: 2 = 15,5 см.

Рассмотрим ΔОНК - прямоугольный .

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

$cos OKH = \dfrac{HK}{OK } ;\\\\cos OKH = \dfrac{15,5}{16 } = \dfrac{155}{160 } = \dfrac{31}{32 }$

Рассмотрим ΔОРК  и найдем ОР по теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

$\\OP ^{2} =PK^{2} +OK^{2} -2\cdot PK\cdot OK \cdot cos OKH;\\\\OP ^{2} =16^{2} +16^{2} -2\cdot 16\cdot16 \cdot \dfrac{31}{32} ;\\\\OP ^{2} =16^{2} +16^{2} -16\cdot31;\\\\OP ^{2} =16\cdot (16+16-31);\\\\OP ^{2} =16\cdot 1;\\ OP ^{2} =16;\\OP =4$

Расстояние от точки Р  до центра окружности равно 4 см.

#SPJ1