Предмет: Математика,
автор: ramdolphin25
Найти производную функции срочно
Приложения:
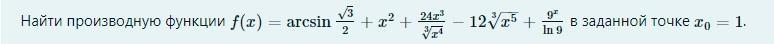

Ответы
Автор ответа:
1
Ответ:
Применяем правила дифференцирования сложных функций и таблицу производных .
Похожие вопросы
Предмет: Математика,
автор: iguzichko10
Предмет: Физика,
автор: Susjushejs
Предмет: Алгебра,
автор: sashahomishena
Предмет: География,
автор: radalina058
Предмет: Биология,
автор: yifyegukno