Предмет: Математика,
автор: gggggggg420hhv
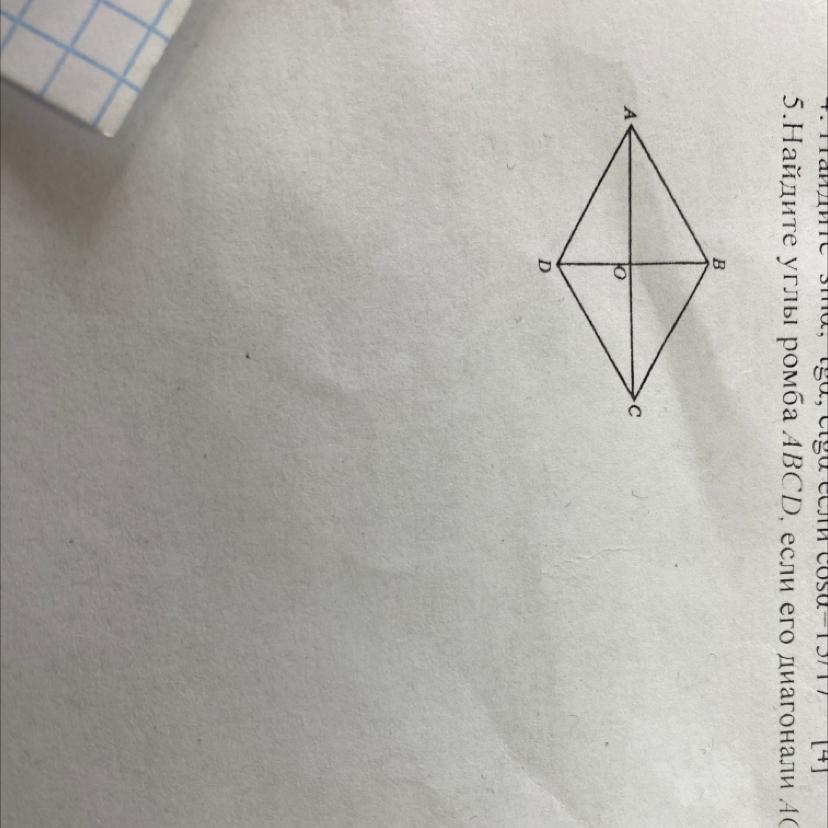
5.Найдите углы ромба ABCD, если его диагонали АС и BD равным 4√3 и 4
В
4
D
с
[
Приложения:
Ответы
Автор ответа:
0
Пошаговое объяснение:
АС=4√3
ВD=4
диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам.
Диагонали ромба являются биссектрисами его углов.
∆АОВ - прямоугольный:
АО=АС:2=4√3:2=2√3
ВО=ВD:2=4:2=2
tg(∠A/2)=BO/AO=2/(2√3)=1/√3
∠A/2=30°
∠А=30•2=60°
В ромбе соседние углы дополняют друг друга до 180°:
∠В=180-∠А=180-60=120°
В ромбе противоположные углы равны, значит
∠С=∠А=60°
∠D=∠B=120°
ответ: 60° ; 120° ; 60° ; 120
Похожие вопросы
Предмет: История,
автор: sofialord590
Предмет: Алгебра,
автор: elzasneznaa711
Предмет: Математика,
автор: Alqoritmika
Предмет: Русский язык,
автор: kotmot7070