Предмет: Геометрия,
автор: Magut
помогиитеее пожалуйста
Приложения:
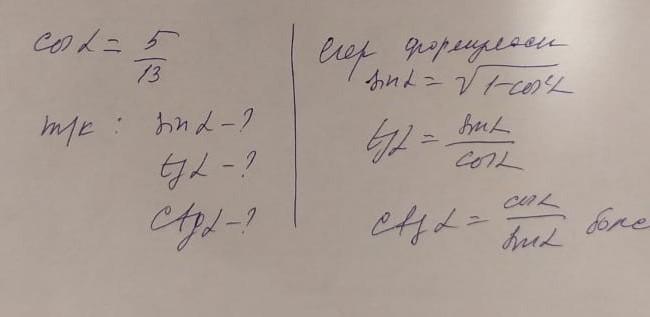
Ответы
Автор ответа:
1
Так как cos A > 0, т.е. угол А лежит в I и IV четвертях, то знаки в этих четвертях для остальных тригонометрических функций разные
Автор ответа:
2
Дано: Найти:
Решение. Применим тождества:
Подставляем и считаем.
- это ответы.
Magut:
спасибо большое!
Похожие вопросы
Предмет: Математика,
автор: stasevskymatvey
Предмет: Математика,
автор: alenalytsyk
Предмет: Английский язык,
автор: Myphon
Предмет: Английский язык,
автор: nastya5365