Предмет: Математика,
автор: Kolanna
даю 90 балів
Знайти похідні
на обведені номерки 14,18,22 не звертайте увагу то просто номер завданнь)
Приложения:
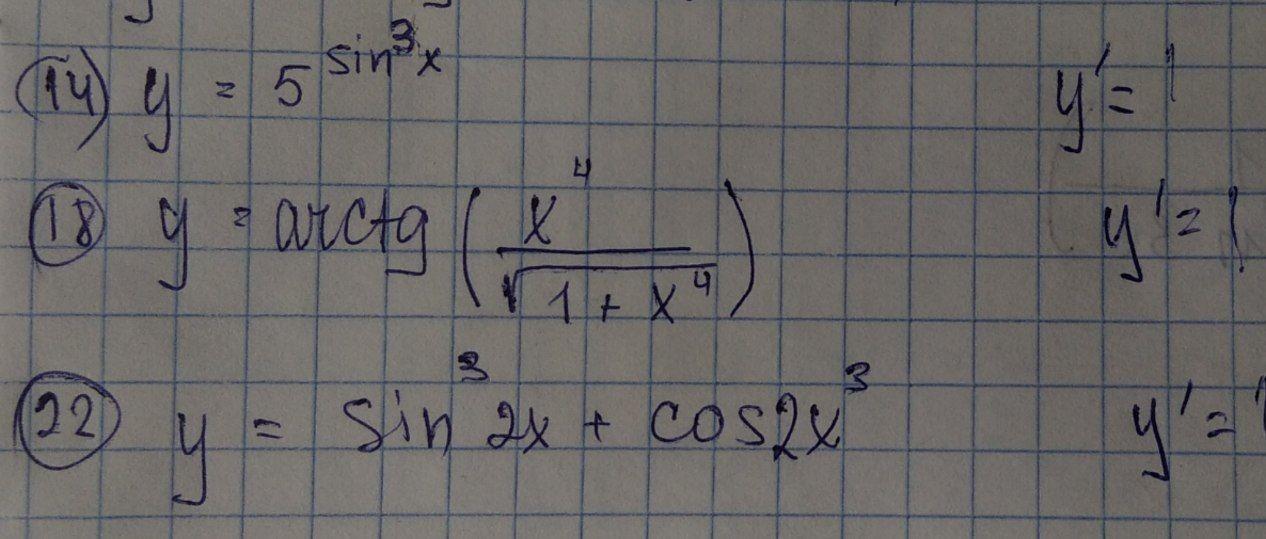
Ответы
Автор ответа:
2
Ответ:
14.
18.
22.
Пошаговое объяснение:
Найти производную.
Имеем производную сложной функции.
14.
18.
22.
Kolanna:
ВЕЛИЧЕЗНЕ ДЯКУЮ!
Похожие вопросы
Предмет: Химия,
автор: skaminsk228
Предмет: Математика,
автор: vikakrishina08
Предмет: Математика,
автор: patruha0901diana
Предмет: География,
автор: Lilia23112006
Предмет: Французский язык,
автор: romalubimov5957