Предмет: Геометрия,
автор: leranikolova761
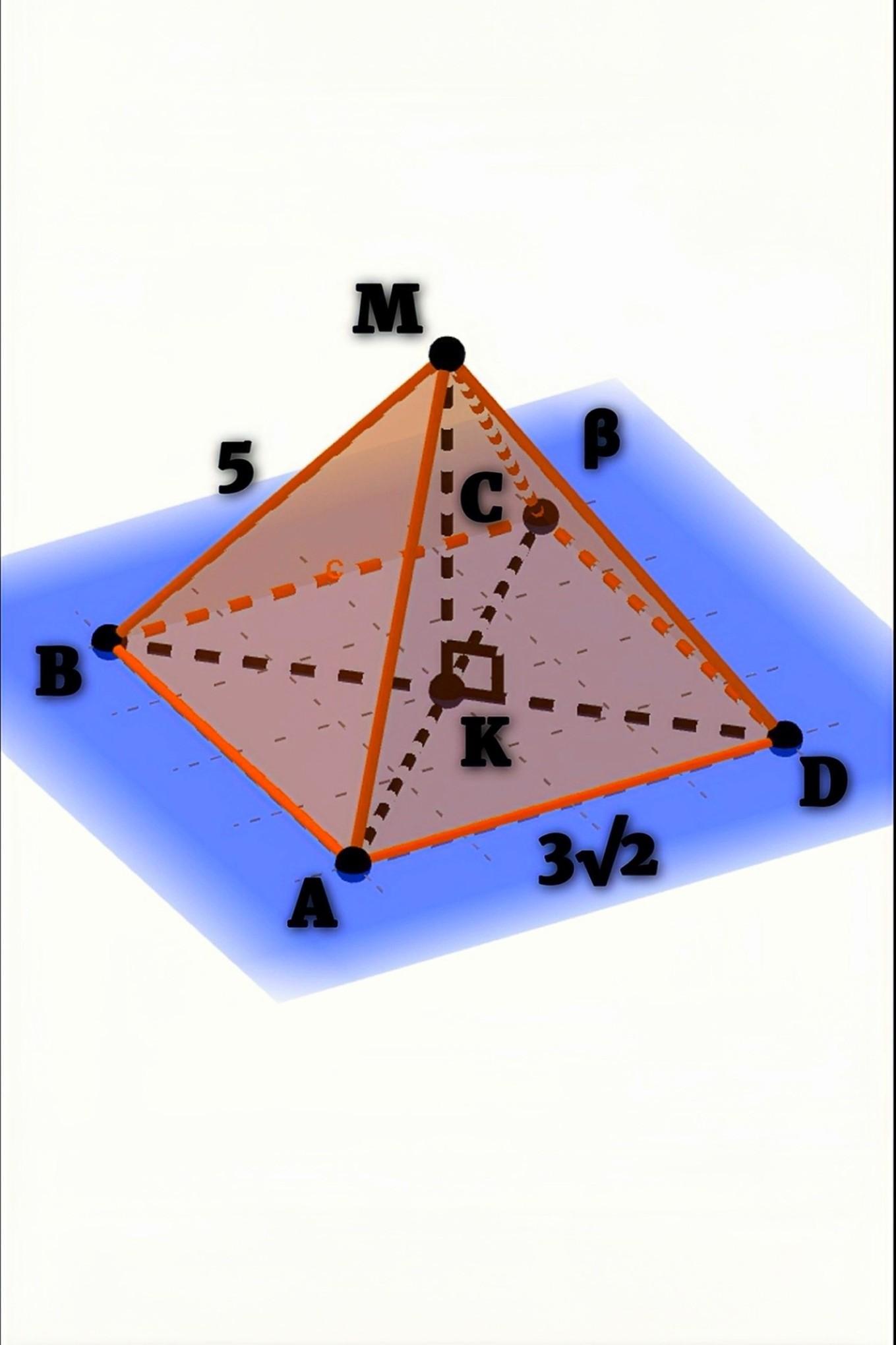
Расстояние от точки М до всех вершин квадрата равно 5 см. Найдите расстояние от точки М до плоскости квадрата, если сторона квадрата равна 3√2 см.
Приведите полное решение задачи.
Помогите пожалуйста
Ответы
Автор ответа:
2
Дано: АВСD - квадрат, M ∉ β, МВ = МА = МС = МD = 5см, СD = 3√2см
Найти: Р(М;β)
⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение
- Расстояние от точки до плоскости – это длина перпендикуляра, опущенного из данной точки на плоскость.
- Опустим перпендикуляр МК на плоскость β. Р(М;β) = МК. Рассмотрим ∆МКD – прямоугольный (∠МКD - прямой). MD - наклонная и она по условию равна 5см. КD - проекция этой наклонной и ещё половина диагонали квадрата, которая лежит в основании правильной четырехугольной пирамиды. Стороны квадрата известны, тогда диагональ BD = 3√2 * √2 = 6см. Т.к. диагонали точкой пересечения делятся пополам, KD = 3см. Теперь найдем само расстояние по Т.Пифагора: МК² = МD² - KD² = 5²- 3² = 25 - 9 = 16. MK = √16 = 4см.
Ответ: Р(М;β) = 4см.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: kykymdrellapiw
Предмет: Алгебра,
автор: alesazebrov
Предмет: Биология,
автор: akkazievansar05
Предмет: Право,
автор: keekkeoe