Предмет: Алгебра,
автор: tpoxodoshuk
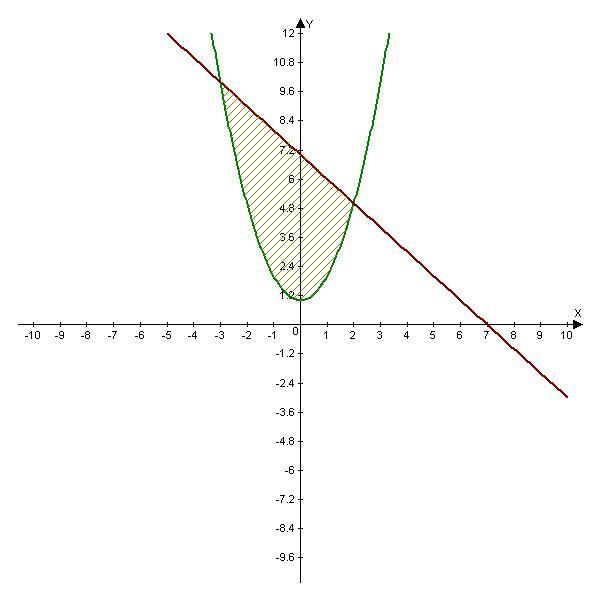
Задано функції f(x)= x² +1 i g(x)= 7-x. Обчисліть площу фігури, обмеженої графіками функцій /(x) i g(x).
Ответы
Автор ответа:
5
- парабола, ветви направлены вверх. Координаты вершины параболы
.
- прямая, проходящая через две точки
Найдем точки пересечения двух графиков функций, приравнивая их функции.
Площадь фигуры, ограниченной линиями:
Приложения:
Похожие вопросы
Предмет: История,
автор: irishhhh
Предмет: Литература,
автор: vika2689087
Предмет: Английский язык,
автор: marychkaw
Предмет: Литература,
автор: zhannadkru
Предмет: Английский язык,
автор: as2120019