Срочно.
В рівнобедреному трикутнику АВС з основою ВС бісектриса ВL вдвічі більше висоти AD. Знайдіть кути трикутника.
Ответы
Ответ:
∠C = 36° , ∠A = 108° , ∠B = 36°
Объяснение:
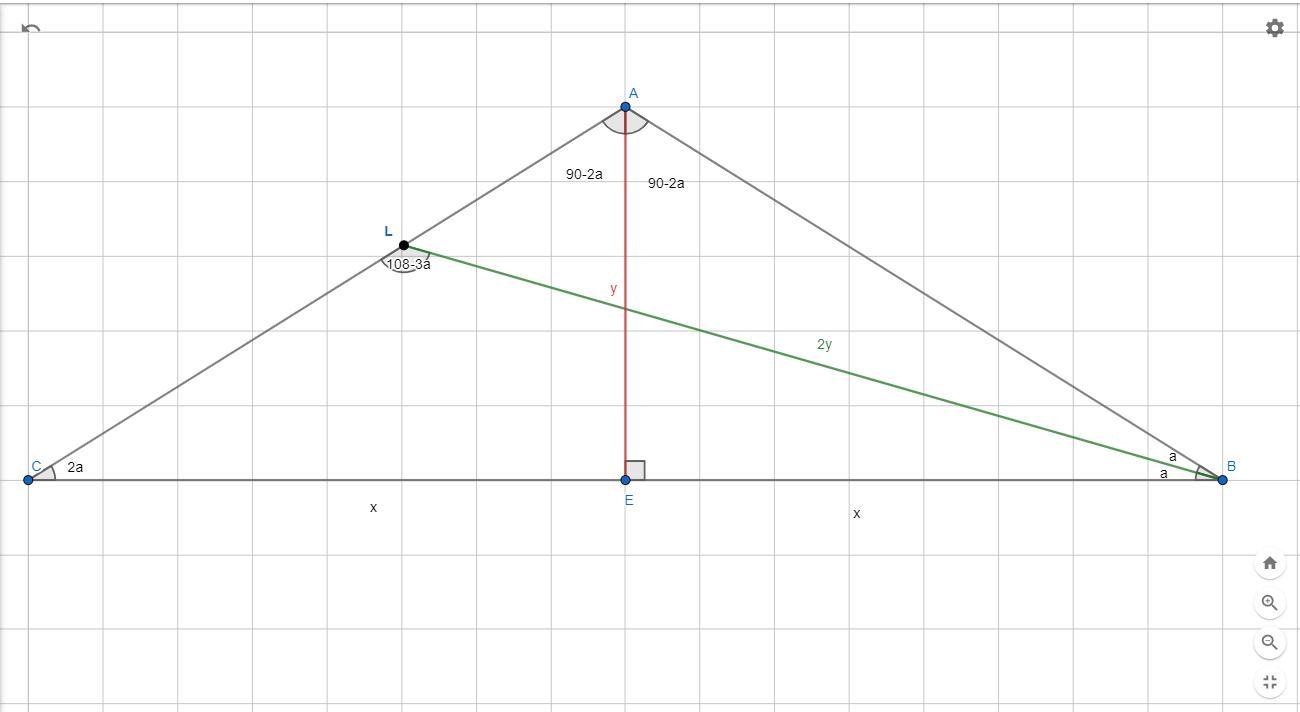
AE - высота
BL - биссектриса
Пусть биссектриса BL делит ∠B на два угла равных a , и далее выводим
∠C = 2a
∠CLB = 180 -3a
∠EAB = 90 - a
Обозначим :
BL = 2y
AE = y
Рассмотрим ΔAEB
Применим Теорему синусов :
Теперь рассмотрим ΔCLB , также применяем Теорему синусов :
И мы получим :
Учтем что
Таким образом 45 не является корнем данного уравнения , методом подбора можно найти корень a = 18°
Либо же пойти данным путем
Применим формулы :
И мы получим :
Введем замену :
Применяем схему Горнера
корень sin a = t = 1 мы не учитываем , т.к 0<a<45
Остается решить уравнение
D = 4 + 16 = 20
берем только положительный корень
Находим угол a
Таким образом данный треугольник имеет углы :
2a = 36° , 180 - 4a = 108° , 2a = 36°
#SPJ1