Предмет: Алгебра,
автор: kabinkasabinka
Помогите пожалуйста!!
Приложения:
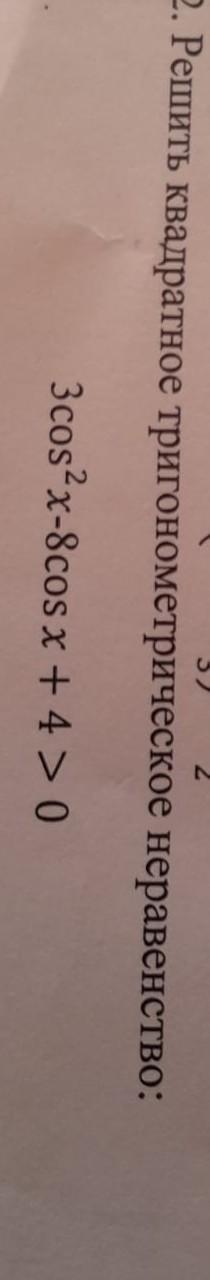
Ответы
Автор ответа:
2
Ответ:
x∈(arccos 2/3 + 2πn ; 2π-arccos 2/3 + 2πn),n∈Z
Объяснение:
2.Решить квадратное тригонометрическое неравенство: 3cos²x - 8cosx + 4 > 0
Пусть cosx = t , где t∈[-1;1] , т.е:
Найдём нули через дискриминант:
Следовательно , t∈(-∞;2/3)U(2;+∞) , это можно включить в совокупность неравенств уже с обратной заменой:
Очевидно , что второе неравенство не имеет решений , тогда решим первое:
Ответ: x∈(arccos 2/3 + 2πn ; 2π-arccos 2/3 + 2πn),n∈Z
Похожие вопросы
Предмет: Алгебра,
автор: boryspimenow
Предмет: Математика,
автор: kirillkovtsenkov
Предмет: Литература,
автор: andrezw555
Предмет: Обществознание,
автор: maximdolgov07
Предмет: Геометрия,
автор: Aisberc