Предмет: Алгебра,
автор: Lettuce13
Сколько корней имеет уравнение
Приложения:
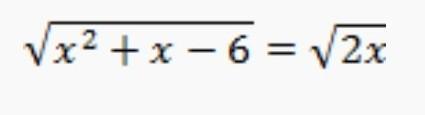
Ответы
Автор ответа:
0
Ответ:
Один корень
Объяснение:
Подкоренные выражения должны быть неотрицательны, поэтому корень х₂=-2 - лишний.
Данное уравнение имеет единственный корень: х=3
Автор ответа:
0
Для того, чтобы найти сколько действительных корней имеет уравнение, нужно решить его.
√(х²+х-6)=√(2х)
Возведём обе части в квадрат:
х²+х-6=2х
х²+х-6-2х=0
х²-х-6=0
D=(-1)²-4*1*(-6) = 1+24 = 25
х₁ ₂ = (-(-1)±√25) / (2*1)
х₁ = (1+5) / 2 = 3
х₂ = (1-5) / 2 = -2
Сделаем проверку:
1) Подставим х₁:
√(3²+3-6) = √2*3
√6=√6
х₁ является действительным корнем уравнения
2) Подставим х₂:
√((-2)²+(-2)-6) = √2*(-2)
√(-4) = √(-4)
х₂ - это не действительный корень уравнения
Ответ: 1 действительный корень
Похожие вопросы
Предмет: Українська мова,
автор: bulateckadarina
Предмет: Математика,
автор: vvladimirova50
Предмет: Геометрия,
автор: ulkopolina27
Предмет: Литература,
автор: kosinskayasasha