886. Решите систему неравенств: a) (2(x-1) - 3(x - 2) < x, 16x - 3 0,6 (10x + 1), 1,6 – 4,5 (4x - 1) < 2x + 26,1; - B) (5,8(1 - a) - 1,8 (6 - a) < 5, 18-4 (2-5a) > - (5a + 6); г) (x (x - 1) - (x2 - 10) < 1-6x, 3,5-(x-1,5) < 6-4x. I (p-8).
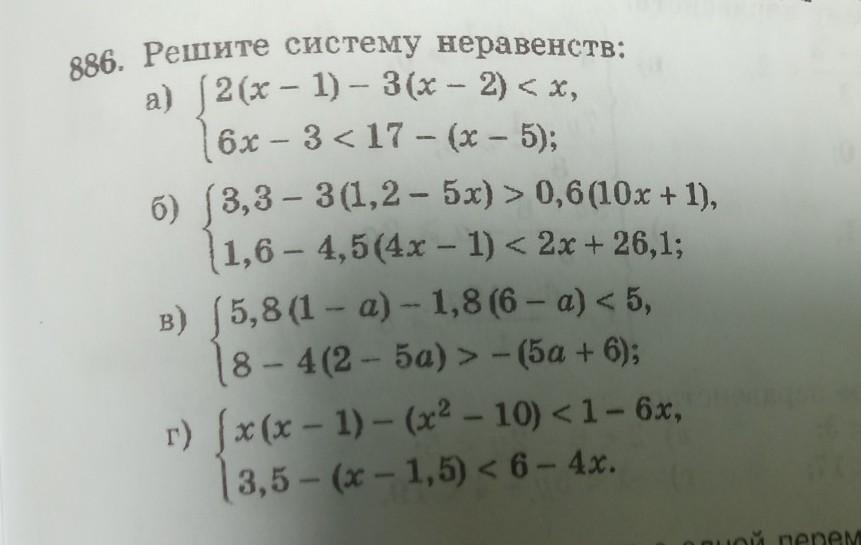
Ответы
Ответ:
Пошаговое объяснение:
a) Начнем с упрощения левой части неравенства:
2(x-1) - 3(x-2) < x
2x - 2 - 3x + 6 < x
-x + 4 < x
4 < 2x
2x > 4
x > 2
Теперь рассмотрим правую часть:
16x - 3 0,6(10x + 1) < 2x + 26,1
16x - 1,8(10x + 1) < 2x + 26,1
16x - 18x - 1,8 < 2x + 26,1
-2x < 45,9
x > -22,95
Итак, система неравенств имеет решение: 2 < x < -22,95.
б) Начнем с упрощения левой части первого неравенства:
5,8(1-a) - 1,8(6-a) < 5
5,8 - 5,8a - 10,8 + 1,8a < 5
-4a < -1,6
a > 0,4
Теперь рассмотрим правую часть второго неравенства:
18 - 4(2 - 5a) > -(5a + 6)
18 - 8 + 20a > -5a - 6
15a > -4
a > -4/15
Итак, система неравенств имеет решение: a > 0,4 и a > -4/15. Поскольку это два неравенства, то решением будет наименьшее из чисел, удовлетворяющих им обоим: a > 0,4.
в) Начнем с упрощения левой части первого неравенства:
x(x-1) - (x^2 - 10) < 1 - 6x
x^2 - x - x^2 + 10 < 1 - 6x
x + 6x < 9
7x < 9
x < 9/7
Теперь рассмотрим правую часть второго неравенства:
3,5 - (x - 1,5) < 6 - 4x
3,5 - x + 1,5 < 6 - 4x
-5x < 1
x > -1/5
Итак, система неравенств имеет решение: -1/5 < x < 9/7.