Предмет: Алгебра,
автор: luckaaviktoria48
2. Решите неравенство
Приложения:
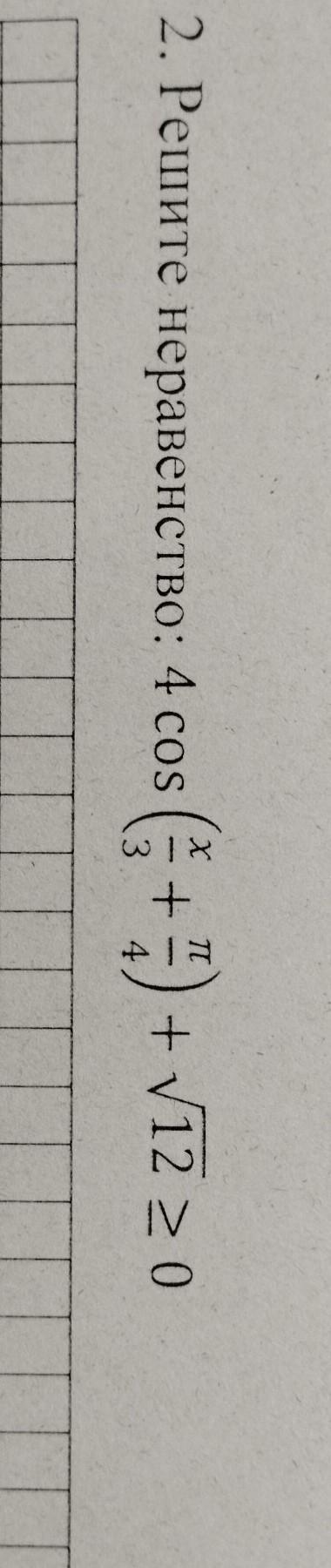
Ответы
Автор ответа:
4
Решите неравенство:
⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение
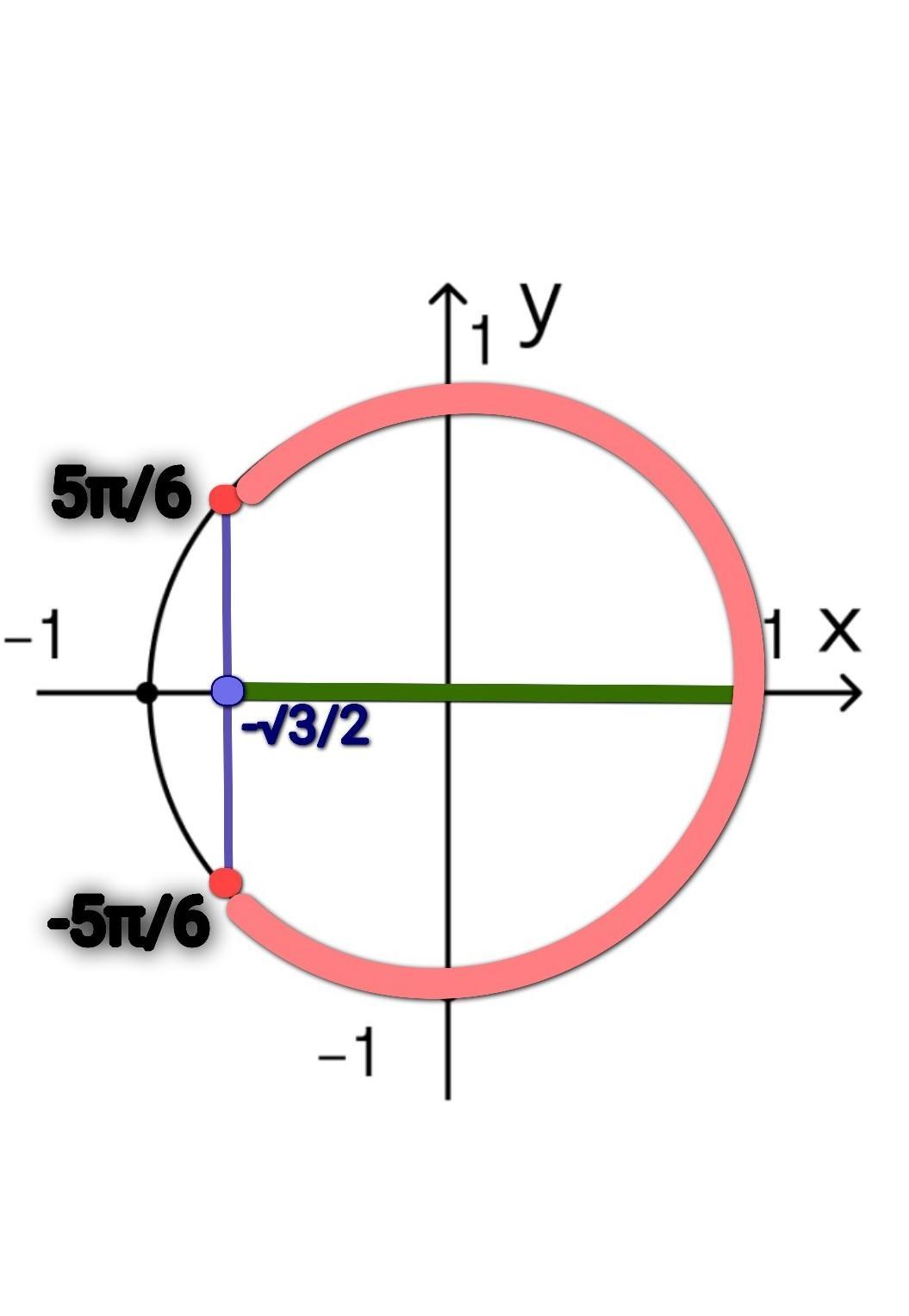
Рассмотрим единичную окружность.
- На оси Ох отметим -√3/2(синяя точка). По условию нас интересуют значения косинуса, большие -√3/2(зелёная область). Найдем дуги, которые нам соответствуют (красная дуга). На окружности есть 2 серии точек, в которых косинус равен -√3/2( красные точки). Запишем все это дело в виде двойного неравенства, учитывая период косинуса.
Приложения:
Похожие вопросы
Предмет: История,
автор: maxglavatskyi
Предмет: Информатика,
автор: Аноним
Предмет: Алгебра,
автор: htao29914
Предмет: Литература,
автор: dolesa345gmacom