Question

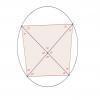
Знайдіть кути чотирикутника АВСD, вписаного в коло, якщо кут ADB=43°, кут ACD=37°, кут CAD=22°​

Answer 1

Відповідь:<A = 100°; <B = 59°; <C = 80°; <D = 121°

Пояснення:Дано:

<ADB = 43°;

<ACD = 37°;

<CAD = 22°.

Знайти: <A, <B, <C, <D.

Розв’язок:

Нехай т.О - точка перетину діагоналей чотирикутника.

<DCA = <DBA = 37° (вписані кути, що спираються на одну дугу, рівні)

<DBC = <DAC = 22°

<AOD = 180° - 22° - 43° = 115°

<AOD + <AOB = 180°  <=>  <AOB = 180° - 115° = 65°

<OAB = 180° - 65° - 37° = 78°

<A = 22° + 78° = 100°

<COD = <AOB = 65°

<CDO = 180° - 65° - 37° = 78°

<D = 78° + 43° = 121°

<ACB = 180° - 115° - 22° = 43°

<C = 37° + 43° = 80°

<B = 22° + 37° = 59°

Перевірка (у вписаного чотирикутника в коло сума протилежних кутів рівна):

<A + <C = <B + <D

100° + 80° = 59° + 121°

180° = 180°