помогите пожалуйста
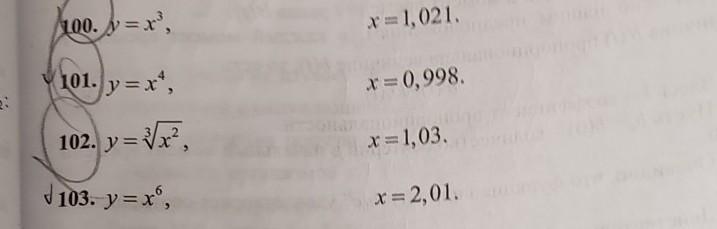
Ответы
Ответ:
100) f(1,021) = 1,063.
101) f(0,998) = 0,992.
102) f(1,03) = 1,02
103) f(2,01) = 65,92
Объяснение:
Вычислить приближенное значение функции.
100)
Ближайшая точка к 1,021, в которой легко вычислить значение функции и ее производной это 1.
Тогда х₀ = 1, тогда Δх = х - х₀ = 1,021 - 1 = 0,021
1. Найдем приращение функции Δf(x₀).
- Δf(x₀) = f'(x₀) · Δx.
2. Найдем приближенное значение функции.
- f(x₀ + Δx) ≈ f(x₀) + Δf(x₀)
f(x₀) = f(1) = 1³ = 1
f(1,021) ≈ 1 + 0,063 = 1,063.
Остальные делаем аналогично.
101)
х₀ = 1, тогда Δх = х - х₀ = 0,998 - 1 = -0,002
1. Найдем приращение функции Δf(x₀).
- Δf(x₀) = f'(x₀) · Δx.
2. Найдем приближенное значение функции.
- f(x₀ + Δx) ≈ f(x₀) + Δf(x₀)
f(x₀) = f(1) = 1⁴ = 1
f(0,998) ≈ 1 - 0,008 = 0,992.
102)
х₀ = 1, тогда Δх = х - х₀ = 1,03 - 1 = 0,03
1. Найдем приращение функции Δf(x₀).
- Δf(x₀) = f'(x₀) · Δx.
2. Найдем приближенное значение функции.
- f(x₀ + Δx) ≈ f(x₀) + Δf(x₀)
f(x₀) = f(1) = ∛1² = 1
f(1,03) ≈ 1 + 0,02 = 1,02
103)
х₀ = 2, тогда Δх = х - х₀ = 2,01 - 2 = 0,01
1. Найдем приращение функции Δf(x₀).
- Δf(x₀) = f'(x₀) · Δx.
2. Найдем приближенное значение функции.
- f(x₀ + Δx) ≈ f(x₀) + Δf(x₀)
f(x₀) = f(2) = 2⁶ = 64
f(2,01) ≈ 64 + 1,92 = 65,92