Question

Будь ласка!
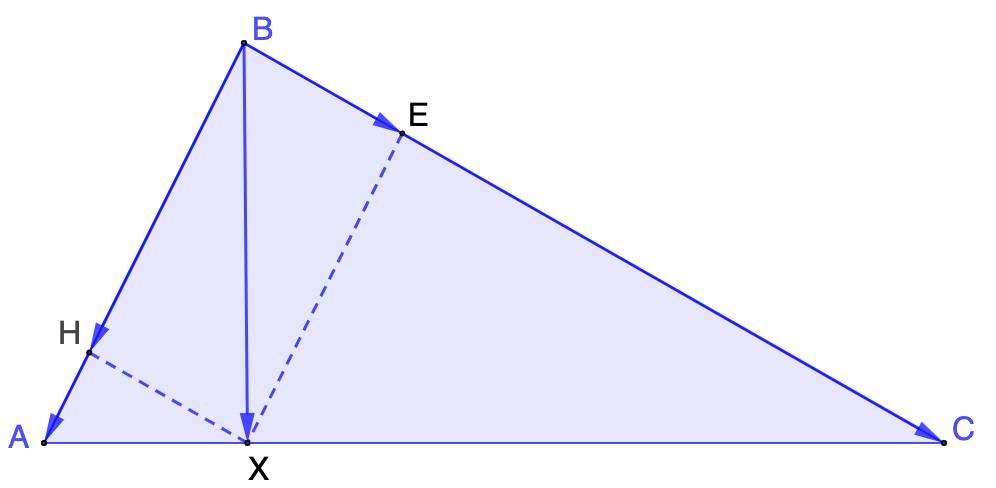
На стороні АС трикутника АВС позначено точку Х так, що AX:XC = 2:7. Доведіть, що вектор BX = (7/9векторBA+2/9векторBC). Виконайте рисунок.

Answer 1

Ответ:

Доказано, что   $\displaystyle \overrightarrow{BX} =\frac{7}{9}\overrightarrow{BA} +\frac{2}{9}\overrightarrow{BC}$

Объяснение:

На стороне АС треугольника AВС отметили точку Х так, что AX : XC = 2 : 7. Доказать, что вектор BX = 7/9 вектора ВА + 2/9 вектора ВС.

Дано: ΔАВС;

Х ∈ АС; АХ : ХС = 2 : 7;

Доказать:

$\displaystyle \overrightarrow{BX} =\frac{7}{9} \overrightarrow{BA} +\frac{2}{9} \overrightarrow{BC}$

Доказательство:

Проведем EX || AB,   HX || BC.

⇒ HBEX - параллелограмм.

Рассмотрим ΔХЕС и ΔАВС.

EX || AB

• Лемма. Если две стороны треугольника пересекает прямая, параллельная третьей стороне, то она отсекает треугольник, подобный данному.

⇒  ΔХЕС ~ ΔАВС    

Запишем отношение сходственных сторон:

$\displaystyle \frac{EX}{BA}=\frac{CX}{CA}$

АХ : ХС = 2 : 7 ⇒ AX = 2 части, ХС = 7 частей; АC = 9 частей.

$\displaystyle \frac{EX}{BA}=\frac{7}{9}\\\\EX=\frac{7}{9} BA$

Рассмотрим ΔАНХ и ΔАВС.

HX || BC

⇒  ΔАНХ ~ ΔАВС    

Запишем отношение сходственных сторон:

$\displaystyle \frac{HX}{BC}=\frac{AX}{AC}$

AX = 2 части, АХ = 9 частей.

$\displaystyle \frac{HX}{BA}=\frac{2}{9}\\\\HX=\frac{2}{9} BA$

• В параллелограмме противоположные стороны равны.

⇒

$\displaystyle EX = BH=\frac{7}{9} BA\\\\HX=BE=\frac{2}{9} BC$

Получили:

$\displaystyle \overrightarrow{BH} =\frac{7}{9}\overrightarrow{BA}\\\\ \overrightarrow{BE}=\frac{2}{9}\overrightarrow{BC}$

По правилу параллелограмма:

$\displaystyle \overrightarrow{BX}= \overrightarrow{BH}+ \overrightarrow{BE}$

или

$\displaystyle \overrightarrow{BX} =\frac{7}{9}\overrightarrow{BA} +\frac{2}{9}\overrightarrow{BC}$

Что и требовалось доказать.

#SPJ1