Предмет: Геометрия,
автор: olanskijtaras818
дано 1 =2
довести :a b
Приложения:
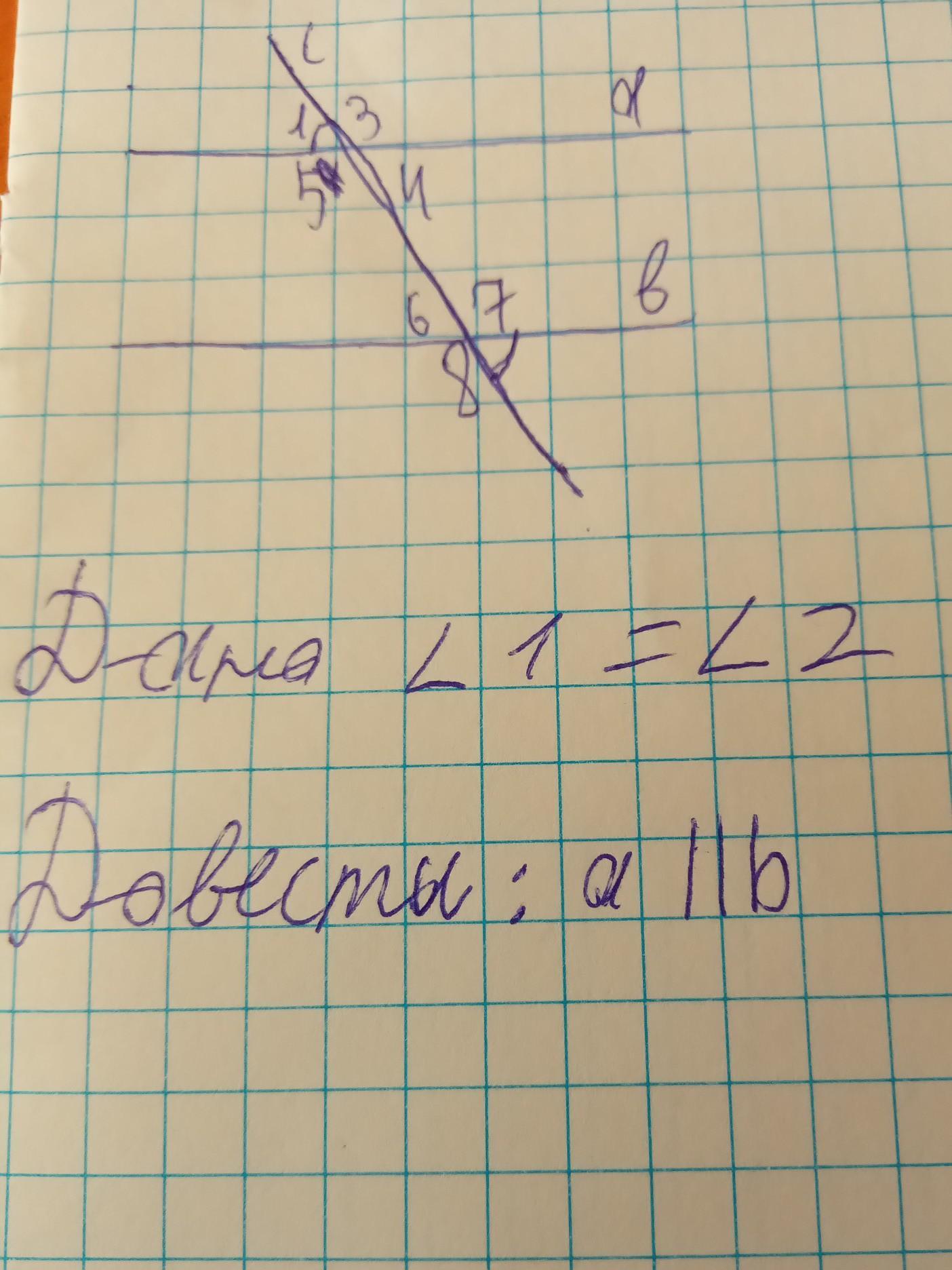
Ответы
Автор ответа:
1
Якщо ∠1 = ∠2, тоді ∠4 = ∠6.
Доведемо цю ознаку.
Якщо при перетині прямих a і b прямою c внутрішні різносторонні кути рівні, то прямі a і b паралельні.
Наприклад, якщо ∠4=∠6, то a∥b.
1. Позначимо точки C і D, у яких прямі a і b перетинає пряма c. Через середину відрізка CD точку K цього відрізка проведемо перпендикуляр AB до прямої a.
2. ∠CKA = ∠DKB як вертикальні кути, ∠4= ∠6= α, CK=KD, отже ΔCKA = ΔDKB за ознакою про сторону та два кути.
3. Зрозуміло, що якщо ΔCKA прямокутний, то й ΔDKB прямокутний, і AB перпендикулярний до прямої b.
4. Прямі, перпендикулярні до однієї й тієї самої прямої, є паралельними (відповідно до першої доведеної ознаки).
Доведемо цю ознаку.
Якщо при перетині прямих a і b прямою c внутрішні різносторонні кути рівні, то прямі a і b паралельні.
Наприклад, якщо ∠4=∠6, то a∥b.
1. Позначимо точки C і D, у яких прямі a і b перетинає пряма c. Через середину відрізка CD точку K цього відрізка проведемо перпендикуляр AB до прямої a.
2. ∠CKA = ∠DKB як вертикальні кути, ∠4= ∠6= α, CK=KD, отже ΔCKA = ΔDKB за ознакою про сторону та два кути.
3. Зрозуміло, що якщо ΔCKA прямокутний, то й ΔDKB прямокутний, і AB перпендикулярний до прямої b.
4. Прямі, перпендикулярні до однієї й тієї самої прямої, є паралельними (відповідно до першої доведеної ознаки).
olanskijtaras818:
Спасибо
Не за что
Похожие вопросы
Предмет: Геометрия,
автор: ostrovskijzena13721
Предмет: Окружающий мир,
автор: anna24shishman
Предмет: Алгебра,
автор: vitaliksmart2
Предмет: Українська література,
автор: kristikkrustik
Предмет: Українська мова,
автор: solosenkoyulia00