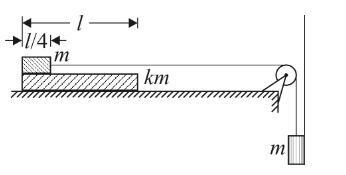
Брусок массой m лежит на доске массой km, как показано на рисунке. Доска располагается на гладком горизонтальном столе, а брусок соединен с грузом массой m с помощью невесомого блока и невесомой нерастяжимой нити, отрезок которой от блока до бруска горизонтален. Коэффициент трения между поверхностями доски и бруска μ = 0,3. Груз удерживают так, что нить слегка натянута, и в некоторый момент времени отпускают из состояния покоя. Пренебрегая трением между поверхностью доски и столом, а также трением в оси блока, определите расстояние Δx, на которое сместится доска за время, в течение которого брусок будет находиться на доске всей своей поверхностью, если k = 2, длина доски l = 85.0 см, а длина бруска равна l/4.
Ответы
Дано:
m1 = m3 = m
m2 = km
k = 2
l1 = l/4
l = 85 см = 0,85 м
μ = 0,3
g = 10 H/кг
Δx - ?
Решение:
Найдём ускорение, с которым брусок начинает скользить по доске относительно стола (с этим же ускорением груз движется вниз):
По Второму закону Ньютона:
m3g - T = m3a3
T - Fтр = m1a1
mg - T = ma
T - μmg = ma
Суммируем:
ma + ma = mg - T + T - μmg
2ma = mg - μmg
2ma = mg(1 - μ)
a = (g/2)*(1 - μ)
Сила трения, действующую на брусок, является равнодействующей силой для доски:
Fтр = m2a2
μmg = kma2
Выразим ускорение доски:
a2 = μg/k
Остаётся выразить ускорение, с которым движется брусок относительно доски, и время, за которое крайняя правая точка бруска достигнет конца доски.
а(о) = а1 - а2 = а - а2 = (g/2)*(1 - μ) - μg/k = g*(1/2)*(1 - μ - μ/k)
Длина пути известна:
s = l - l/4 = l*(1 - 1/4) = (3/4)*l, тогда выражаем квадрат времени:
s = a(o)t²/2 => t² = 2s/a(o) = 2*(3/4)*l / [g*(1/2)*(1 - μ - μ/k)]
Значит, расстояние, на которое сместится доска за время t:
Δx = a2t²/2 = { (μg/k)*2*(3/4)*l / [g*(1/2)*(1 - μ - μ/k)] } /2 = (μl/k)*(3/4) / [(1/2)*(1 - μ - μ/k)] = 3μl/(2k*(1 - μ - μ/k)) = 3*0,3*0,85/(2*2*(1 - 0,3 - 0,3/2)) = 0,9*0,85/(4 - 1,2 - 0,6) = 0,765/2,2 = 0,34772... м = 34,7 cм
Ответ: 34,7 см.