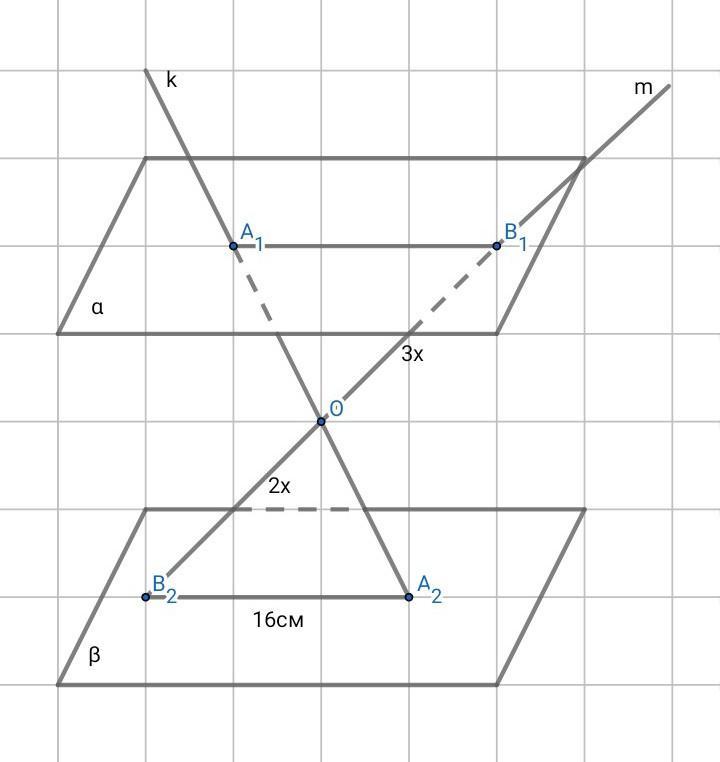
Через точку О, що лежить поза двома паралельними площинами α і β, проведено дві прямі k і m. Пряма k перетинає площини α і β в точках А1 і А2 відповідно, пряма m – в точках В1 і В2. Знайдіть довжину відрізка А1В1, якщо А2В2 = 16см, О В1 : В1В2 = 3:5.
Ответы
Через точку О, лежащую вне двух параллельных плоскостей α и β, проведены две прямые k и m. Прямая k пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А1В1, если А2В2 = 16см, ОВ1 : В1В2 = 3:5.
============================
Дано: А₂В₂ = 16см, ОВ₁:В₁В₂ = 3:5
Найти: А₁В₁ – ?
⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение
∠А₂ОВ₂ = ∠А₁ОВ₁ – вертикальные.
∠А₂В₂О = А₁В₁О – внут. накрест лежащие
∠В₂А₂О = В₁А₁О – внут. накрест лежащие.
Следовательно ∆А₂ОВ₂ ~ ∆А₁ОВ₁.
Сделаем соотношение:
см.
Ответ: А₁В₁ =  см.
см.

Ответ:
A₁B₁ = 24см
Объяснение:
Дано:
α||β
k∩α=A₁ ; k∩β=A₂
m∩α=B₁ ; m∩β=B₂
A₂B₂=16см
ОВ₁:В₁В₂=3:5
Найти:
А₁В₁
Решение:
Если параллельные плоскости пересечены секущей k и m , то ∠B₁A₁A₂ = ∠B₂A₂A₁ также ∠А₁В₁В₂ = ∠А₂В₂В₁(как внутренние накрест-лежащие) , а ∠А₁ОВ₁ = ∠В₂ОА₂(как вертикальные) , тогда ∆А₁ОВ₁~∆В₂ОА₂ по 3-ём углам.
Пусть OB₁ = 3x , a B₁B₂ = 5x , тогда ОВ₂ = В₁В₂ - ОВ₁ = 5х - 3х = 2х. Запишем отношение сходственных сторон (как правило , это стороны лежащие против равных углов) , затем найдём А₁В₁: