Предмет: Алгебра,
автор: zellinna
Допоможіть будь ласка
Приложения:
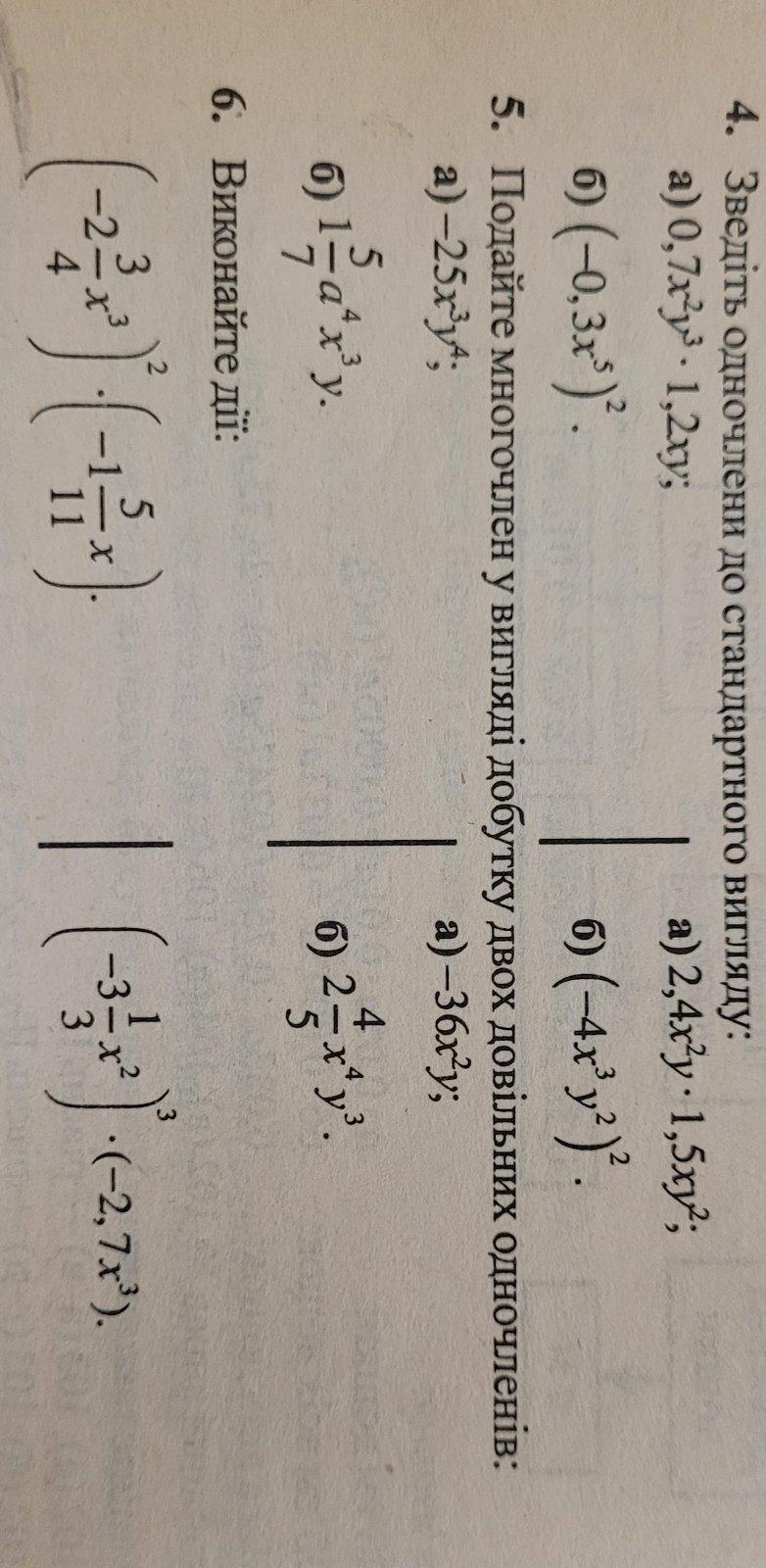
Ответы
Автор ответа:
0
Объяснение:
какой ты класс? если что смогу помочь думаю
Автор ответа:
1
Ответ:
Применяем свойства степеней: .
1) Привести одночлены к стандартному виду .
2) Представить в виде произведения двух сомножителей .
3) Выполнить действия .
Похожие вопросы
Предмет: Українська література,
автор: vika0542545
Предмет: Физика,
автор: Аноним
Предмет: Английский язык,
автор: viktoriatop02
Предмет: Английский язык,
автор: durachok49