Предмет: Геометрия,
автор: misstatyana2310
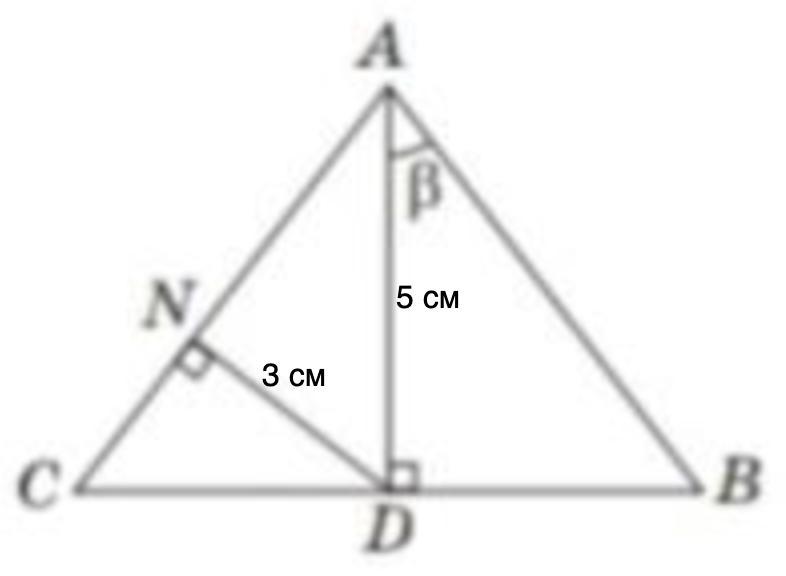
У трикутнику АВС проведено висоту AD, з точки D опущено перпендикуляр DN на сторону АС (рис. 3). Знайдіть площу трикутника АВС, якщо AD = 5 см, DN = 3 см, кут BAD = b
Приложения:

Ответы
Автор ответа:
5
Ответ:
Площадь треугольника АВС равна cм².
Объяснение:
В треугольнике АВС проведена высота AD, из точки D опущен перпендикуляр DN на сторону АС (рис. 3). Найдите площадь треугольника АВС, если AD = 5 см, DN = 3 см, угол BAD = β.
Дано: ΔАВС;
АD - высота;
DN ⊥ AC;
AD = 5 см, DN = 3 см, угол BAD = β.
Найти: S(ABC)
Решение:
- Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне.
1. Рассмотрим ΔDAB - прямоугольный.
- Тангенс - отношение противолежащего катета к прилежащему.
(см)
(см²)
2. Рассмотрим ΔNAD - прямоугольный.
По теореме Пифагора найдем AN:
AN² = AD² - ND² = 25 - 9 = 16
AN = √16 = 4 (см)
3. Рассмотрим ΔCAD - прямоугольный.
DN ⊥ AC.
- Воспользуемся метрическими соотношениями в прямоугольном треугольнике: Квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу.
AD² = AN · AC
25 = 4 · AC
(см)
(см²)
4. Площадь ΔАВС можно найти как сумму площадей ΔADB и ΔACD:
#SPJ1
Приложения:
Похожие вопросы
Предмет: Литература,
автор: 5310Polly
Предмет: Литература,
автор: Аноним
Предмет: Экономика,
автор: Vvv2245
Предмет: Математика,
автор: mtursunmamet