Question

СРОЧНО!!! Сторони чотирикутника, вписаного в коло, дорівнюють відповідно АВ =
1 см, ВС = 2 см, CD = 3 Смі AD = 1 см. Знайдіть діагональ BD

Answer 1

Ответ:

$\dfrac{5\sqrt{7} }{7}$  см.

Объяснение:

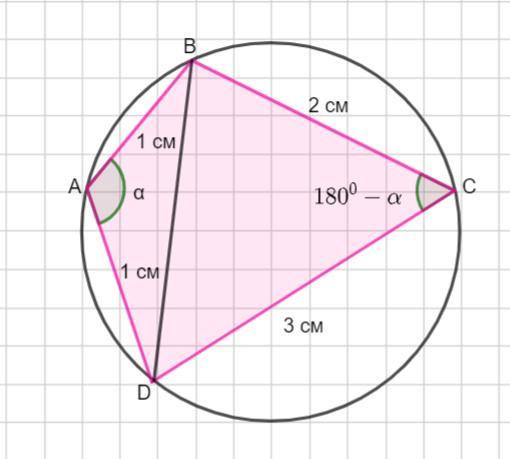
Стороны четырехугольника, вписанного в окружность, равны АВ =1 см, ВС =2 см, СD =3 см, AD =1 см. Найти диагональ ВD.

Пусть четырехугольник ABCD  вписан в окружность. Тогда сумма противоположных углов равна 180°. Значит, ∠А +∠С =180°. Пусть ∠А =α. Тогда ∠С =180°-α. Проведем диагональ ВD .

Рассмотрим ΔАВD и ΔВСD.

Применим теорему косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

ΔАВD

$BD^{2} =AB^{2} +AD^{2} -2\cdot AB\cdot AD \cdot \cos \alpha ;\\\\BD^{2} =1^{2} +1^{2} -2\cdot 1\cdot 1 \cdot \cos \alpha=1+1-2\cdot \cos\alpha =2-2\cdot \cos\alpha .$

ΔВСD

Воспользуемся равенством      $\cos(180^{0} -\alpha )=-\cos\alpha$

$BD^{2} =BC^{2} +CD^{2} -2\cdot BC\cdot CD \cdot \cos(180^{0} - \alpha ) ;\\\\BD^{2} =2^{2} +3^{2} -2\cdot 2\cdot 3 \cdot \cos (180^{0} -\alpha)=4+9+12\cdot \cos\alpha =13+12\cdot \cos\alpha .$

Тогда получим уравнение

$2-2\cdot \cos\alpha =13+12\cdot \cos \alpha ;\\-2\cdot \cos\alpha -12\cdot \cos \alpha=13-2;\\-14\cos\alpha =11;\\\\\cos\alpha =-\dfrac{11}{14}$

Найдем диагональ ВD.

$BD^{2} =2-2\cdot \left(-\dfrac{11}{14}\right )=2+\dfrac{11}{7} =\dfrac{14+11}{7} =\dfrac{25}{7} ;\\\\BD =\sqrt{\dfrac{25}{7} } =\dfrac{5}{\sqrt{7} } =\dfrac{5\sqrt{7} }{7}$

Значит, диагональ ВD равна $\dfrac{5\sqrt{7} }{7}$   см

#SPJ1