Предмет: Алгебра,
автор: Kapcake3
Розв'язати рівняння:.
Приложения:
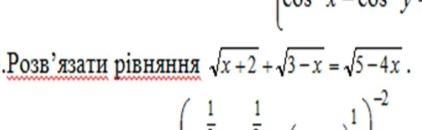
Ответы
Автор ответа:
3
Ответ: x = -1
Объяснение:
ОДЗ :
Возведем обе части в квадрат
Если у квадратного уравнения ax² + bx + c =0
a - b + c = 0 ⇒ одним из корней является - 1
Т.к 5 - (-1) - 6 =0 ⇒ x₁ = - 1 , a x₂ найдем по теореме Виета
Ввиду ограничения x ≤ 0 , у нашего уравнения имеется только корень x = - 1
Похожие вопросы
Предмет: Математика,
автор: savenk0helen0
Предмет: История,
автор: ivaula64
Предмет: Физика,
автор: Miroslava2288
Предмет: История,
автор: dimarudenko444