Question

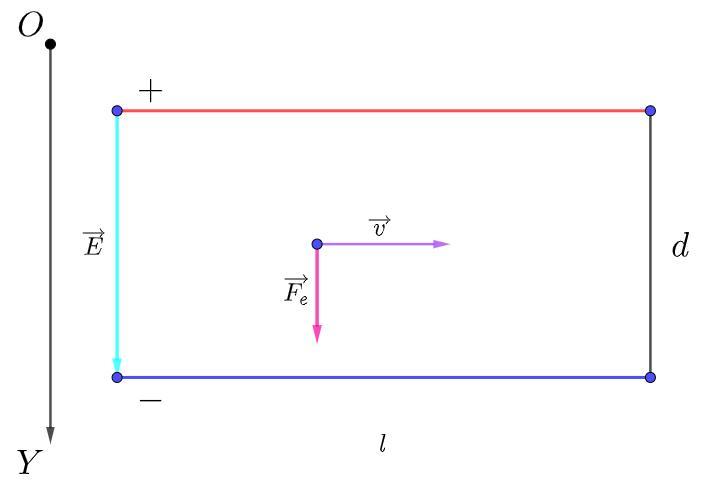
СРОЧНО 100БАЛЛОВ Пучок электронов пройдя ускоряющую разность потенциалов 2 B влетает между обкладками конденсатора параллельно им посередине Какое максимальное напряжение надо подать на обкладки этого конденсатора чтобы пучок мог вылететь ИЗ КОНДЕНсатора отклонившись от своего первоначального направления на максимальный угол Длина конденсатора (=10 см. расстояние между обкладками d = 1см​

Answer 1

Ответ:

На обкладки конденсатора необходимо подать напряжение 40 В

Примечание:

Следуем, именно условию фотографии, поэтому считаем, что пучок электронов прошел разность 2000 В.

Сила тяжести намного меньше других сил действующих на электрон, поэтому ней можно пренебречь.

Считаем, что начальная скорость пучка электронов 0 м/c

Объяснение:

Дано:

$\Delta \phi =$ 2000 В

$l =$ 0,1 м

$d =$ 0,01 м

Найти:

$U \ - \ ?$

---------------------------------

Решение:

Кинетическая энергия электрона:

$W = \dfrac{mv^{2}}{2}$

Работа есть изменение энергии:

$A = \Delta W$ (в данном случае, можно написать, что $A = W$, так как начальная скорость электрона (до прохождения разности потенциалов) считаем равной нулю)

Работа электрического поля:

$A = q\Delta \phi$

$\dfrac{mv^{2}}{2} = q\Delta \phi \Longrightarrow v^{2} = \dfrac{2 q\Delta \phi}{m}$

Движение электрона в конденсаторе:

$\displaystyle \left \{ {{OX: l = vt|:v} \atop {OY: \dfrac{d}{2} = \dfrac{at^{2}}{2} \bigg | \cdot 2 }} \right \left \{ {{t = \dfrac{l}{v} } \atop {d = at^{2}}} \right \Longrightarrow d = \dfrac{al^{2}}{v^{2}} \Longrightarrow \boxed{ a = \frac{dv^{2}}{l^{2}} }$

Модуль силы действующей со стороны электрического поля на электрон в конденсаторе:

$F_{e} = qE$

По второму закону Ньютона:

$\overrightarrow{F_{e}} = m \vec{a}$

$OY:qE = ma \Longrightarrow E = \dfrac{ma}{q} = \dfrac{ \dfrac{mdv^{2}}{l^{2}} }{\dfrac{q}{1} } = \dfrac{mdv^{2}}{ql^{2}}$

Напряжение в конденсаторе:

$U = Ed = \dfrac{md^{2}v^{2}}{ql^{2}} = \dfrac{\dfrac{2 q md^{2} \Delta \phi}{m}}{\dfrac{ql^{2}}{1} } = \dfrac{2 q md^{2} \Delta \phi}{mql^{2}} = \dfrac{2d^{2} \Delta \phi}{l^{2}}$

$\boldsymbol{\boxed{U= \dfrac{2d^{2} \Delta \phi}{l^{2}}}}$

Расчеты:

$\boldsymbol U =$ (2 · 0,0001 м² · 2000 В) / (0,01 м²) = 40 В

Ответ: $U =$ 40 В.