Question

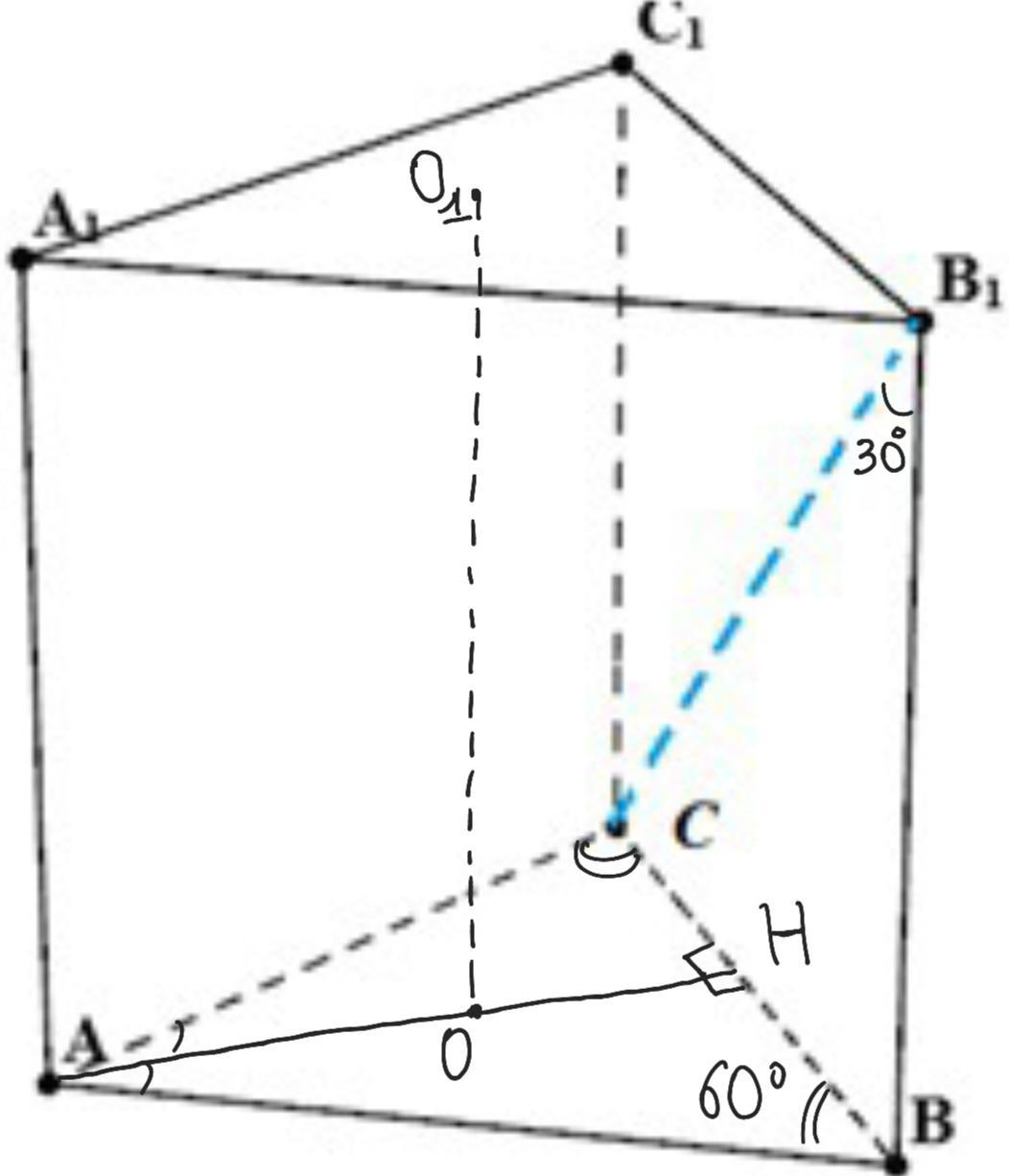
Висота основи правильної трикутної призми дорівнює 2см.
Знайдіть площу бічної поверхні цієї призми, якщо діагональ
бічної грані призми утворює з її бічним ребром кут 30 ◦ .

Answer 1

Дано: АВСА1В1С1 — правильная треугольная призма, АН — высота ВАС, АН= 2см, В1С — диагональ С1В1ВС, ∠СВ1В=30°.

Найти: Sбок. поверх. призмы.

Решение.

1) В ΔАНВ (∠АНВ=90°, ∠НВА=60°, т.к. АВСА1В1С1 — правильная треугольная призма, значит, ΔАВС - равностор.):

tg60°= AH/HB;

√3= 2/НВ;

НВ√3= 2;

НВ= 2/√3= (2√3)/3 (см).

В равностороннем треугольнике, высота также является медианой и биссектрисой, значит, АН — это также медиана, а значит, СН=НВ.

Отсюда, CB= 2HB= (4√3)/3 (см).

2) В ΔСВВ1:

tg30°= CB/B1B;

√3/3= (4√3)/3B1B;

3B1B√3= 12√3;

3B1B=12;

B1B= 4 (см).

3) Sбок. поверх. правильной треугольной призмы = 3•а•h, где а — длина стороны, h — длина высоты призмы.

Соответственно, Sбок. поверх. АВСА1В1С1 = 3•СВ•В1В= 3•(4√3)/3 • 4= 4√3•4= 16√3 (см).

Ответ: 16√3 см.

Рисунок приложен.