Question

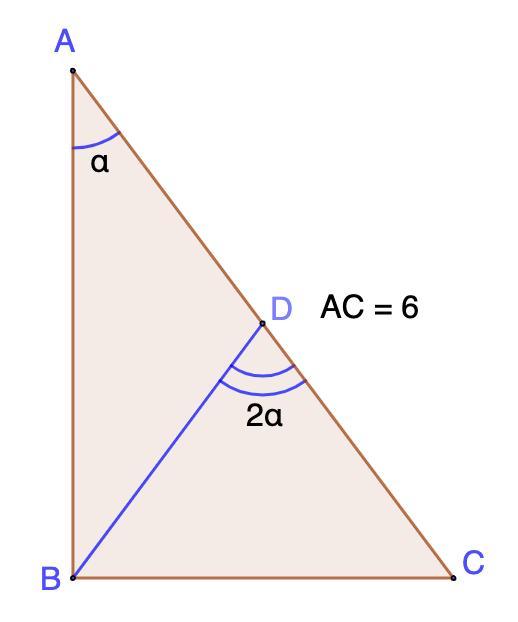
В прямоугольном треугольнике ABC гипотенуза AC равна 6. На стороне AC взята точка D так, что уголь BDC в два раза больше , чем угол BAC. Найдите BD

Answer 1

Ответ:

Отрезок BD равен 3 ед.

Пошаговое объяснение:

В прямоугольном треугольнике ABC гипотенуза AC равна 6. На стороне AC взята точка D так, что уголь BDC в два раза больше , чем угол BAC. Найдите BD.

Дано: ΔАВС - прямоугольный;

АС = 6 - гипотенуза;

D ∈ АС; ∠BDC = 2∠BAC.

Найти: BD.

Решение:

Пусть ∠ВАС = α, тогда ∠BDC = 2α.

Рассмотрим ΔBAD.

∠BDC = 2α - внешний.

• Внешний угол треугольника равен сумме углов, не смежных с ним.

⇒ ∠BDC = ∠BAD + ∠ABD

2α = α + ∠ABD

⇒ ∠ABD = α

• Если в треугольнике два угла равны, то этот треугольник равнобедренный.

⇒ AD = BD     (1)

Рассмотрим ΔBDC.

∠DBC = ∠B - ∠ABD = 90° - α

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠C = 90° - ∠BAC = 90° - α

∠DBC = ∠C

⇒ ΔBDC - равнобедренный.

BD = DC     (2)

Из (1) и (2) следует, что

AD = DC

Значит BD - медиана.

• Медиана, проведенная из вершины прямого угла, равна половине гипотенузы.

⇒ BD = AC : 2 = 6: 2 = 3

Отрезок BD равен 3 ед.

#SPJ1