Предмет: Математика,
автор: bubenco
Хто допоможе - отримає 50 балів
розв'язати рівняння матричним методом
Приложения:
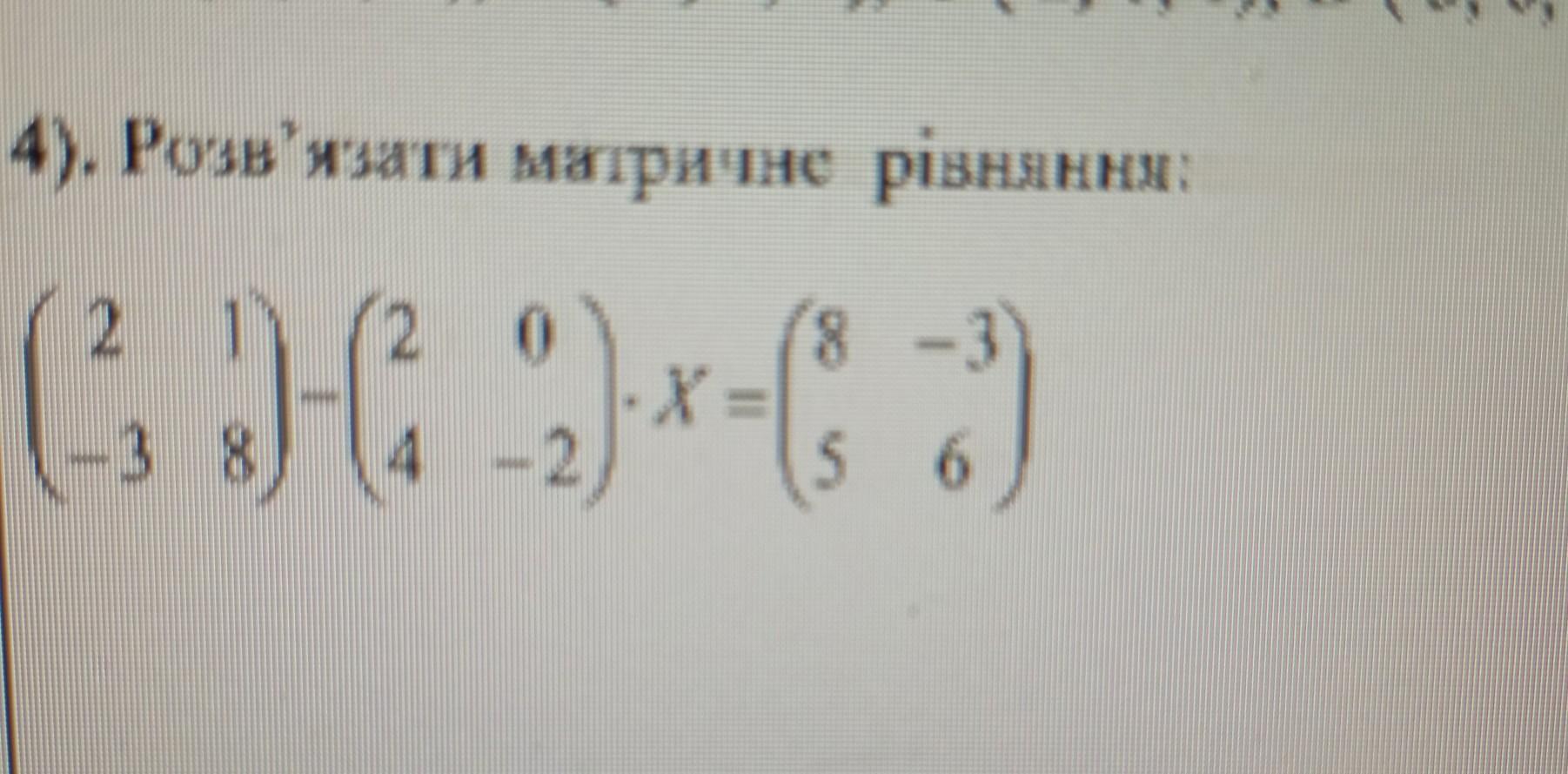
Ответы
Автор ответа:
2
Ответ:
Матричное уравнение . Cначала выразим матрицу Х из уравнения .
Найдём обратную матрицу .
Произведение обратной матрицы на исходную даёт единичную матрицу, поэтому
.
Приложения:


Похожие вопросы
Предмет: Українська мова,
автор: rostyk27
Предмет: Українська мова,
автор: kitty451
Предмет: Немецкий язык,
автор: nasam7
Предмет: Математика,
автор: VarvaraAveryanova
Предмет: Музыка,
автор: hm456