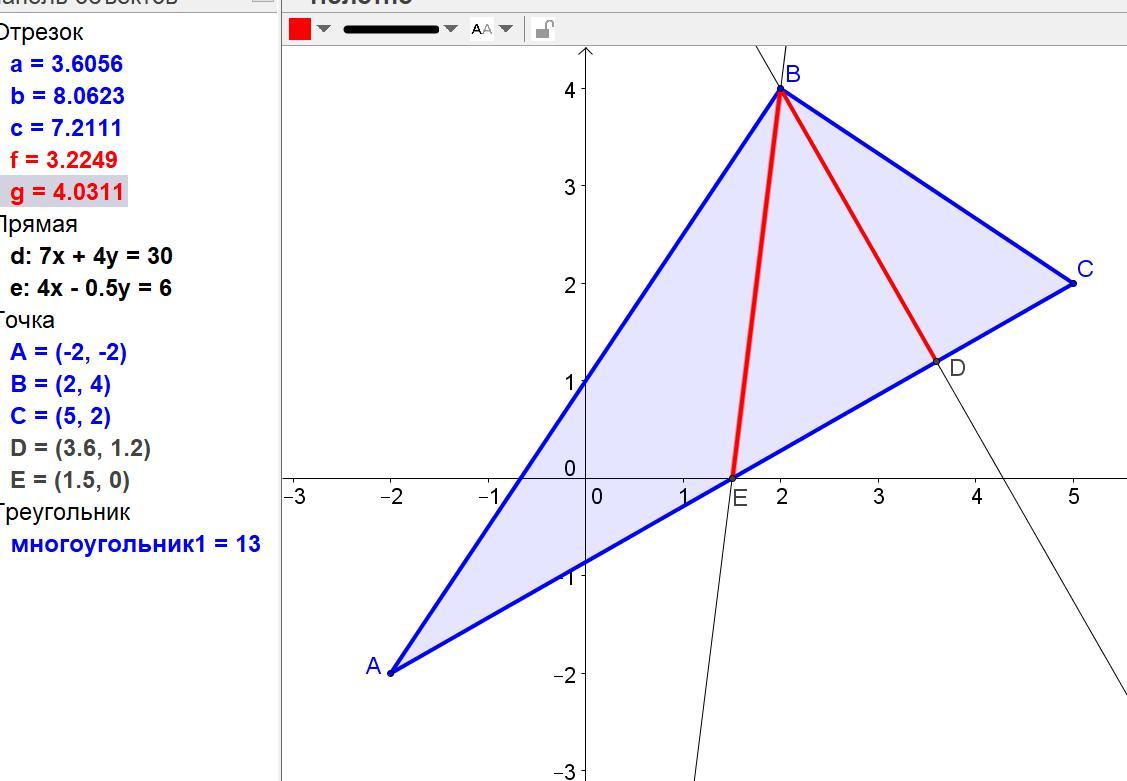
Задано вершини трикутника
A(-2; -2) ,B(2;4 ),C(5;2)
Скласти рівняння висоти, що опущена з вершини B на сторону AC,
і медіани, що проведена з тієї ж вершини.
Ответы
Задано вершини трикутника
A(-2; -2) ,B(2;4 ),C(5;2)
Скласти рівняння висоти, що опущена з вершини B на сторону AC,
і медіани, що проведена з тієї ж вершини.
1) рівняння висоти BD трикутника.
Находим уравнение общего вида Ax + By + C = 0 стороны AС (на которую опущена высота).
Определяем вектор АС по точкам A(-2; -2) и C(5;2)
AC = (5-(-2); 2-(-2)) = (7; 4).
Уравнение АС: (x + 2)/7 = (y + 2)/4 каноническое.
Оно же в общем виде: 4x + 8 = 7y + 14,
4x - 7y - 6 = 0.
У перпендикуляра коэффициенты А и В меняются на B и (-A) или (-В) и А (чтобы произведение равнялось нулю по свойству перпендикулярных векторов).
BD: 7x + 4y + C = 0. Подставим вместо переменных координаты точки B: 7*2 + 4*4 + С = 0, отсюда С = -14 – 16 = -30.
Уравнение BD: 7x + 4y - 30 = 0.
2) Находим координаты точки Е как середину стороны АС.
Е = (А( -2 ; -2 ) + С( 5 ; 2 ))/2 = (1,5; 0).
Вектор BЕ = (1,5-2; 0-4) = (-0,5; -4).
Уравнение BЕ: (x - 2)/(-0,5) = (y - 4)/(-4) каноническое.
Оно же в общем виде: -4x + 8 = -0,5y + 2,
4x - 0,5y - 6 = 0 или 8x - y - 12 = 0.