Предмет: Геометрия,
автор: teamrexsson
Срочно
Найдите углы
равнобедренной трапеции
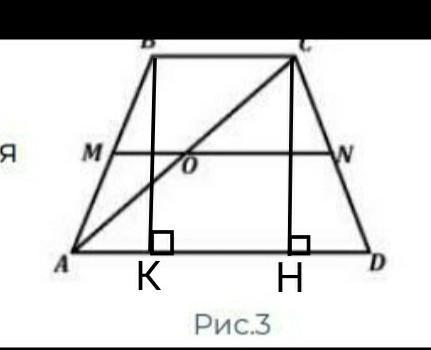
ABCD (рис.3), если MN− ее средняя
линия. MO = 10 см и ON = 35 см, а
боковая сторона равна 50 см.
Приложения:

Ответы
Автор ответа:
1
Ответ:
∠A=60°
∠B=120°
∠C=60°
∠D=120°
Объяснение:
МО- средняя линия треугольника ∆АВС.
ВС=2*МО=2*10=20см
ON- средняя линия треугольника ∆САD
AD=2*ON=2*35=70см
Проведем две высоты ВК и СН.
ВС=КН=20см
АК=НD, трапеция равнобокая
AK=(AD-KH)/2=(70-20)/2=50/2=25см
АК- катет ∆АВК.
АК в два раза больше гипотенузы АВ.
значит ∠АВК=30°, лежит против катета АК.
Сумма острых углов в прямоугольном треугольнике равна 90°
∠ВАК=90°-∠АВК=90°-30°=60°
∠А=60°
Сумма углов прилежащих к боковой стороне трапеции равна 180°
∠В=180°-∠А=180°-60°=120°
В равнобокой трапеции углы при основании равны.
∠А=∠D=60°
∠B=∠C=120°
Приложения:
Похожие вопросы