Question

Помогите пожалуйста срочно нужно!!! Заранее спасибо! Около окружности описан квадрат, а около квадрата описана большая окружность. Радиус меньшей окружности равен 2√2
Найдите площадь круга, описанного около квадрата. Полученный результат поделите на π и запишите в ответ.

Answer 1

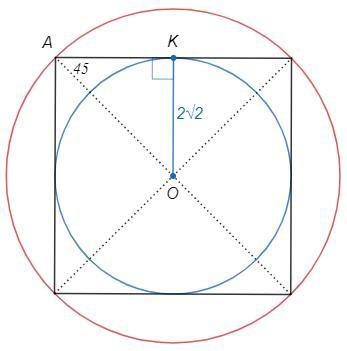
Диагонали квадрата являются биссектрисами его углов.

Точка пересечения диагоналей равноудалена от сторон и является центром вписанной окружности.

Диагонали квадрата равны, точкой пересечения делятся пополам.

Точка пересечения диагоналей равноудалена от вершин и является центром описанной окружности.

Центры coвпадают.

Радиус вписанной окружности OK=2√2

OKA=90 (радиус в точку касания)

KAO=45 (AO - биссектриса)

△AKO с углами 45, 90 - стороны относятся как 1:1:√2

AO =OK*√2 =4

S = п OK^2 =16 п