Предмет: Алгебра,
автор: saman110
Найти производную высшая математика
Приложения:
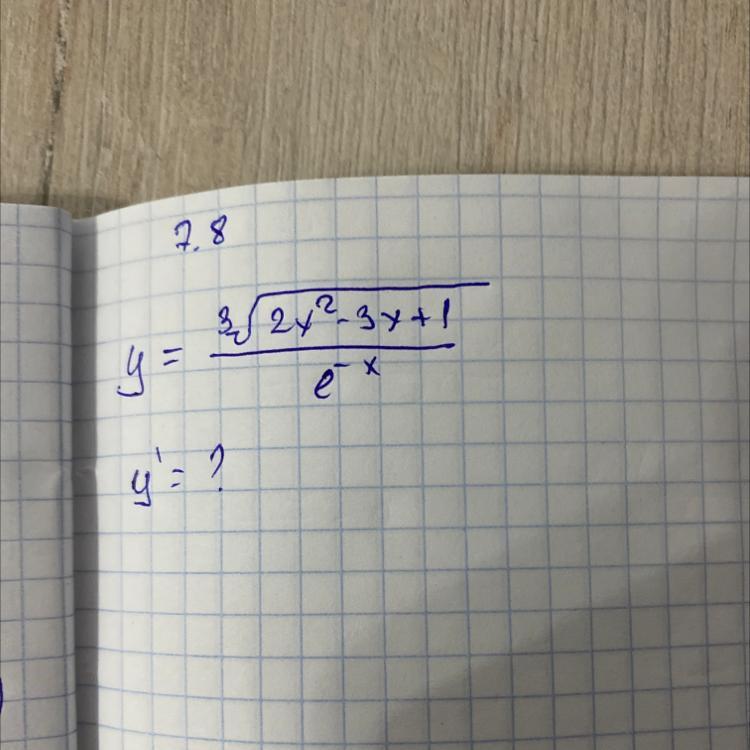
Ответы
Автор ответа:
1
Ответ:
Производная дроби равна ,
linoka2008:
здравствуйте можете мне пожалуйста помочь с алгеброй мне очень нужно пожалуйста
Похожие вопросы
Предмет: Математика,
автор: popcorn82
Предмет: История,
автор: REYZEN8625
Предмет: Окружающий мир,
автор: annzotik3018
Предмет: Литература,
автор: Аноним
Предмет: География,
автор: datentey