Предмет: Геометрия,
автор: Nastya1998Trushkova
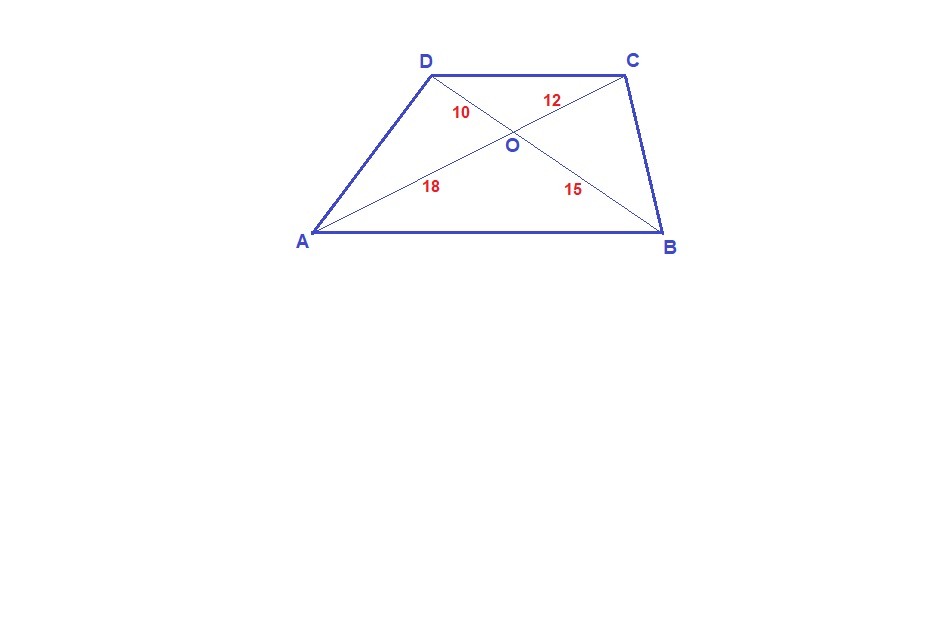
Диагонали АС и ВД четырехугольника АВСД пересекаются в точке О. АО=18 см, ОС=12см, ВО=15см, ОД=10см. Докажите, что АВСД - трапеция.
Ответы
Автор ответа:
0
Рассмотрим треугольники АОВ и COD:
АО : ОС = 18 : 12 = 3 : 2
ВО : OD = 15 : 10 = 3 : 2
∠АОВ = ∠COD как вертикальные, значит
∠АОВ подобен ∠COD по двум пропорциональным сторонам и углу между ними.
В подобных треугольниках напротив пропорциональных сторон лежат равные углы, значит
∠ОАВ = ∠OCD, а эти углы - накрест лежащие при пересечении прямых АВ и CD секущей АС, значит
АВ║CD.
Так как треугольники подобны с коэффициентом 3:2, то АВ ≠ CD, тогда ABCD не является параллелограммом, т.е. две другие стороны у него не параллельны. Значит ABCD - трапеция.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: prostopolona
Предмет: История,
автор: lonelya898
Предмет: Обществознание,
автор: Pain71
Предмет: Математика,
автор: marsel1977