Question

ДОПОМОЖІТЬ
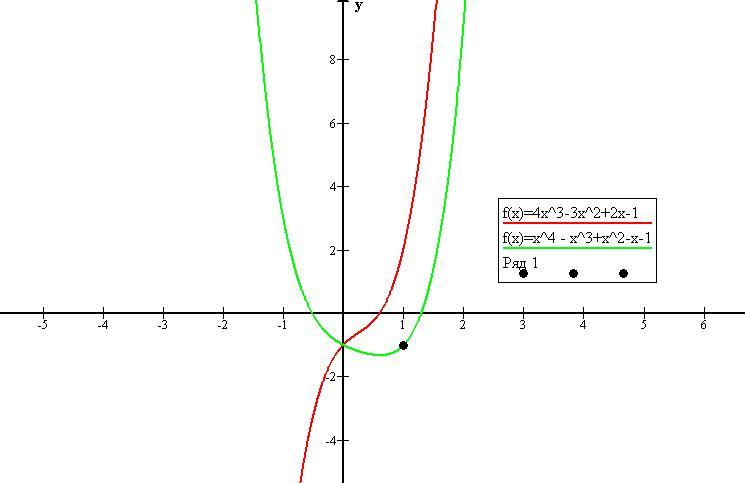
знайти первісну для функції y=f(x), графік якої проходить через точку M(x;y). y=4x³-3x²+2x-1; A(1;-1)

Answer 1

Ответ:

Первообразная, которая проходит через точку А(1;-1), функции у=4х³-3х²+2х-1 имеет вид F(x)=x⁴-x³+x²-x-1.

Объяснение:

Функция довольно простая, для нахождения её первообразной нам понадобится лишь несколько элементарных правил интегрирования:

$\bf \displaystyle \int f(x) \pm g(x) \ dx = \int f(x) \ dx \pm \int g(x)\ dx\\\\ \int C \ dx = C\cdot x+C \\\\ \int x^n \ dx = \frac{x^{n+1}}{n+1} +C \ \big(n\neq(-1)\big)$

Записываем функцию и находим её неопределённый интеграл используя вышеуказанные правила интегрирования.

$\displaystyle y=4x^3-3x^2+2x-1 \\\\ F(x) = \int \big(4x^3-3x^2+2x-1\big) \ dx = \int4x^3\ dx - \int 3x^2 \ dx + \int2x \ dx - \int1\ dx= \\\\= 4\cdot \frac{x^{3+1}}{3+1} -3\cdot \frac{x^{2+1}}{2+1} + 2\cdot \frac{x^{1+1}}{1+1} - 1 \cdot x +C=x^4 - x^3+x^2-x+C$

Мы нашли общий вид первообразных для заданной функции. Это F(x) = x⁴ -x³ + x² - x + C.

Теперь нам нужно найти значение константы С, при котором график этой ф-ции будет проходить через точку А(1;-1) - х=1, у=(-1). Подставляем:

$1^4-1^3+1^2-1+C=(-1) \\\\ 1-1+1-1+C=(-1) \\\\ C= (-1)$

График функции F(x) = x⁴ -x³ + x² - x + C проходит через точку А(1;-1) при значении константы С=(-1).

Первообразная, которая проходит через точку А(1;-1), функции у=4х³-3х²+2х-1 имеет вид F(x)=x⁴-x³+x²-x-1.