Предмет: Алгебра,
автор: yaroslavkalinin2023
СРОЧНО ОЧЕНЬ . НА ФОТО плизззз
Приложения:
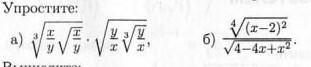
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: topho139
Предмет: Химия,
автор: vinniknatalia0
Предмет: Алгебра,
автор: trusevskijkosta
Предмет: Математика,
автор: pahneeva
Предмет: Алгебра,
автор: yanaprivalova