Даю 50 баллов.
Решение требуется с объяснением!
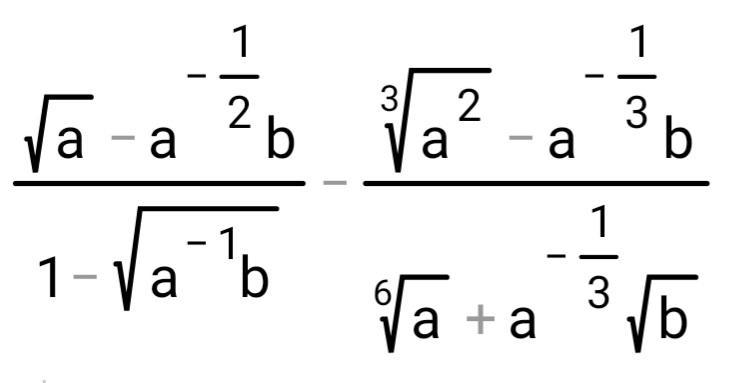
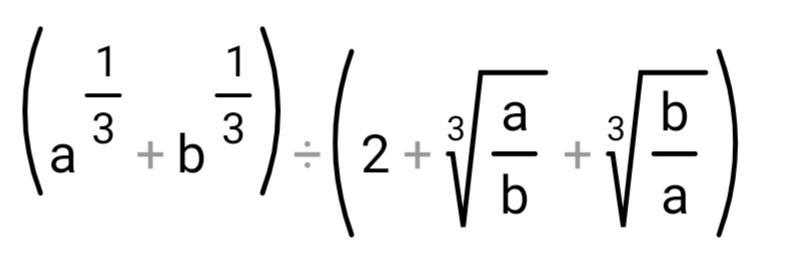
Ответы
Ответ:
Объяснение:
(√a -a^(-1/2) ·b)/(1-√(a⁻¹·b)) -(∛a² -a^(-1/3) ·b)/(⁶√a +a^(-1/3) ·√b)=2√b
1) √a -a^(-1/2) ·b=√a -b/√a=(√a² -b)/√a=(a-b)/√a
2) 1-√(a⁻¹·b)=1 -√(b/a)=(√a -√b)/√a
3) ((a-b)/√a)/((√a -√b)/√a)=(a-b)/√a ·(√a)/(√a -√b)=(a-b)/(√a -√b)
4) ∛a² -a^(-1/3) ·b=∛a² -b/∛a=(∛a³ -b)/∛a=(a-b)/∛a
Пояснение: ∛a² -b/∛a=(a^(2/3 +1/3))/∛a -b/∛a
5) ⁶√a +a^(-1/3) ·√b=⁶√a +(√b)/∛a=(⁶√a³ +√b)/∛a=(√a +√b)/∛a
Пояснение: ⁶√a +(√b)/∛a=(a^(1/6 +1/3))/∛a +√b/∛a
6) ((a-b)/∛a)/((√a +√b)/∛a)=(a-b)/∛a ·(∛a)/(√a +√b)=(a-b)/(√a +√b)
7) (a-b)/(√a -√b) -(a-b)/(√a +√b)=((a-b)(√a +√b)-(a-b)(√a -√b))/((√a -√b)(√a +√b))=((a-b)(√a +√b -√a +√b))/(a-b)=2√b
(a^(1/3) +b^(1/3))÷(2+∛(a/b) +∛(b/a))=(∛(ab))/(∛a +∛b)
1) 2+∛(a/b) +∛(b/a)=2 +(∛a)/∛b +(∛b)/∛a=(∛a² +2∛a ·∛b +∛b²)/(∛a ·∛b)=(∛a +∛b)²/∛(ab)
2) (a^(1/3) +b^(1/3)) ÷(∛a +∛b)²/∛(ab)=(∛a +∛b)·(∛(ab))/(∛a +∛b)²=(∛(ab))/(∛a +∛b)